Рекурсия возникает, если функция или процедура вызывает саму себя. Пря-
мая рекурсия может вызывать себя непосредственно, как в данном примере:
function Factorial (num :Longint) : Longint;
begin
Factorial := num*Factorial(num-i);
end;
Рекурсивная процедура также может вызывать себя косвенно, вызывая вторую
процедуру, которая, в свою очередь, вызывает первую:
procedure Ping(num : Integer);
begin
Pong(num-1);
end;
procedure Pong(num:integer);
begin
Ping(num div 2);
end;
Рекурсия полезна при решении задач, которые могут быть разложены на не-
сколько подзадач. Например, дерево, изображенное на рис. 5.1, можно представить
в виде «ствола», откуда выходят два дерева меньших размеров. Таким образом мож-
но написать рекурсивную процедуру для рисования деревьев.
procedure DrawTree;
begin
// Рисование "ствола"
// Рисование маленького дерева, повернутого на -45 градусов
// Рисование маленького дерева, повернутого на 45 градусов
end;
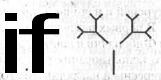
Рис. 5.1. Дерево
Хотя рекурсия и упрощает понимание некоторых явлений, люди обычно мыс-
лят нерекурсивно. Они обычно стремятся разбить сложные задачи на задачи
меньшего объема, которые можно выполнить по порядку одну за другой до полного
завершения. Например, вы начнете красить забор
с одного края и продолжите двигаться в другую
сторону до завершения работы. Скорее всего, во
время выполнения подобной задачи вы даже не
думаете о возможности рекурсивной окраски,-
вначале левой половины изгороди, а затем, рекурно, правой.
Для того чтобы думать рекурсивно, нужно раз-
ложить задачу на подзадачи, которые затем рекур-
сивно разбить на еще меньшие подзадачи. На определенном уровне подзадачи ста-
новятся настолько простыми, что могут быть выполнены непосредственно. Когда
решены все элементарные подзадачи, большие подзадачи, которые из них состав-
лены, также можно считать решенными. Исходная задача окажется выполненной,
когда будут выполнены все образующие ее подзадачи.
http://www.rstelle.ru/vechernie-platja-vechernie-platja-moskva.htm |