Кривые Гильберта (Hilbert curves) - это самоподобные кривые, которые обыч-
но определяются рекурсивно. На рис. 5.2 изображены кривые Гильберта 1-го, 2-го,
и 3-го порядка.
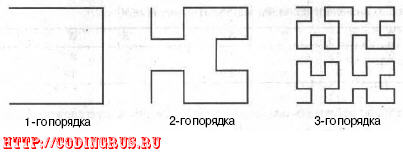
Рис. 5.2. Кривые Гильберта
Кривую Гильберта или любую другую самоподобную кривую можно создать раз-
биением большой кривой на меньшие части. Затем для построения следующих час-
тей необходимо использовать эту же кривую с соответствующим размером и углом
вращения. Полученные части допускается разбивать на более мелкие фрагменты до
тех пор, пока процесс не достигнет нужной глубины рекурсии. Порядок кривой опре-
деляется как максимальная глубина рекурсии, которой достигает процедура.
Процедура Hilbert управляет глубиной рекурсии, используя соответствую-
щий параметр глубины. При каждом рекурсивном вызове процедура уменьшает
данный параметр на единицу. Если процедура вызывается с глубиной рекурсии,
равной 1, она выводит простую кривую 1-го порядка, показанную слева на рис. 5.2,
и завершает работу. Это основное условие остановки рекурсии.
Например, кривая Гильберта 2-го порядка состоит из четырех кривых Гильбер-
та 1-го порядка. Точно так же кривая Гильберта 3-го порядка составлена из четы-
рех кривых Гильберта 2-го порядка, каждая из которых включает четыре кривых
Гильберта 1-го порядка. На рис. 5.3 изображены кривые Гильберта 2-го и 3-го по-
рядка. Меньшие кривые, из которых построены кривые большего размера, выде-
лены жирными линиями.

Рис. 5.3: Кривые Гильберта, составленные из меньших кривых
Следующий код строит кривую Гильберта 1-го порядка:
with DrawArea.Canvas do
begin
LineTo(PenPos.X + Length, PenPos.Y);
LineTofPenPos.X, PenPos.Y + Length);
LineTofPenPos.X - Length, PenPos.Y);
end;
Предполагается, что рисунок начинается с левого верхнего угла области и что
переменная Length для каждого сегмента линии определена должным образом.
Метод для рисования кривой Гильберта более высоких порядков будет вы-
глядеть следующим образом:
procedure Hilbert (Depth : Integer);
begin
if (Depth = 1) then
Рисование кривой Гильберта глубины 1
else
Рисование и соединение четырех кривых Гильберта Hilbert (Depth - 1)
end;
Необходимо слегка усложнить этот метод, чтобы процедура Hilbert могла
определять направление, в каком будет рисоваться кривая - по часовой стрелке
или против. Это требуется для того, чтобы выбрать тип используемых кривых
Гильберта.
Эту информацию можно передать процедуре, добавив параметры dx и dy,
определяющие направление вывода первой линии в кривой. Если кривая имеет
глубину, равную единице, процедура выводит ее первую линию в соответствии
с функцией LineTo ( PenPos . X+dx , PenPos . Y+dy ) . Если кривая имеет большую
глубину, ей то процедура присоединяет первые две меньшие кривые с помощью
вызова LineTo ( PenPos . X+dx , PenPos . Y+dy ) . В любом случае процедура может
использовать dx и dy для того, чтобы определить направление рисования состав-
ляющих кривую линий.
Код Delphi для рисования Гильбертовых кривых короткий, но достаточно слож-
ный. Чтобы точно отследить, как изменяются dx и dy для построения различных
частей кривой, вам необходимо несколько раз пройти этот алгоритм в отладчике
для кривых 1-го и 2-го порядка.
procedure THilblForm.DrawHilbert (depth, dx, dy : Integer);
begin
with DrawArea .Canvas do
begin
if (depth > 1) then DrawHilbert (depth - 1,dy,dx);
LineTo ( PenPos . X+dx , PenPos . Y+dy ) ;
if (depth > 1) then DrawHilbert (depth - 1,dx,dy);
LineTo ( PenPos . X+dy , PenPos . Y+dx) ;
if (depth > 1) then DrawHilbert (depth - 1,dx,dy);
LineTo ( PenPos . X-dx , PenPos . Y-dy ) ;
if (depth > 1) then DrawHilbert (depth - 1,-dy,-dx);
end;
end;
Таблица 5.5. Количество рекурсивных обращений к процедуре Hilbert
 |