(forward star), описанное ранее, обеспе-
чивает компактное представление деревьев, графов и сетей на основе массивов.
Для хранения дерева с помощью метода нумерации связей в массиве FirstLink
записывается индекс первой ветви, исходящей из каждого узла. В другой массив,
ToNode, заносятся узлы, к которым ведет данная ветвь.
Метка в конце массива FirstLink указывает на точку, расположенную сразу
за последним элементом массива ToNode. Это позволяет легко определить, какие
ветви выходят из каждого узла. Ветви, начинающиеся в узле i, указаны под номе-
рами отFirstLink[i] до FirstLink [i+l]-l.
На рис. 6.7 показано дерево и его представление нумерацией связей. Связи от
узла 3 (обозначенного как D) - это ветви от FirstLink [3 ] до FirstLink [4] -1.
Значение FirstLink [3] =9, a FirstLink [4] =11, поэтому эти ветви обозна-
чены как 9 и 10. Записи массива ToNode для них составляют ToNode [ 9 ] =10
и ToNode [10] =11, следовательно, для узла 3 дочерними являются узлы 10 и 11,
обозначенные как К и L. Это означает, что узел D соединен с К и L.
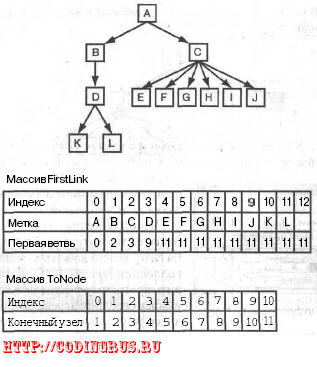
Рис. 6.7. Дерево и его представление нумерацией связей
Представление дерева с помощью метода нумерации связей компактно и ос-
новано на массиве, что облегчает запись и чтение деревьев, представленных та-
ким образом, из файлов. Операции над массивами выполняются быстрее, чем опе-
рации с указателями, необходимые при некоторых других представлениях.
По этой причине большая часть литературы по сетевым алгоритмам использу-
ет представление нумерацией связей. Многие статьи о поиске кратчайшего пути
предполагают, что данные записаны в подобном формате. Прежде чем изучать эти
алгоритмы по журналам, таким как Management Science или Operations Research,
вы должны освоить представление нумерацией связей.
С помощью данного метода можно быстро отыскать ветви, исходящие из опре-
деленного узла. С другой стороны, очень сложно изменять структуру данных,
представленных в таком виде. Чтобы добавить новый дочерний узел к узлу А
(см. рис. 6.7), необходимо изменить практически каждый элемент в массивах
ToNode и FirstLink. Сначала необходимо сдвинуть все элементы в массиве ToNode
на одну позицию вправо, чтобы освободить место для новой ветви, затем вставить
новую запись ToNode, которая указывает на новый узел. И наконец, необходимо про-
смотреть весь массив FirstLink, обновив каждый элемент так, чтобы он указывал
на новую позицию соответствующей записи ToNode. Поскольку все записи ToNode
сдвинулись на одну позицию вправо, чтобы освободить место для новой ветви, нуж-
но добавить единицу ко всем задействованным записям FirstLink.
На рис. 6.8 показано дерево после добавления нового узла. Измененные эле-
менты закрашены серым цветом.
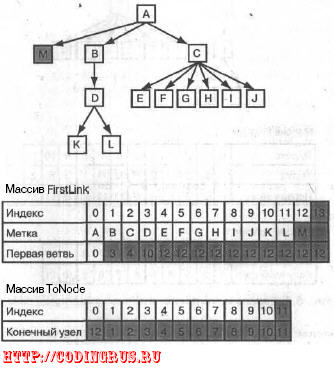
Рис. 6.8. Добавление узла
Удалить узел из начала дерева, представленного нумерацией связей, столь же
трудно, как и добавить. Если удаляемый узел имеет потомков, процесс занимает
еще больше времени, потому что вы также должны удалить и дочерние записи.
Если нужно часто модифицировать дерево, то лучше использовать класс с мас-
сивом или связанным списком указателей на потомков. Такое представление про-
цедур обычно проще понимать и отлаживать. С другой стороны, представление
в виде нумерации связей иногда обеспечивает более высокую производительность
для сложных алгоритмов. Кроме того, это стандартная структура данных, которая
широко освещена в литературе, поэтому вы должны обязательно изучить ее, если
хотите и далее исследовать алгоритмы работы с сетями и деревьями.
Программа FStar использует представление нумерацией связей, чтобы управ-
лять деревом с узлами различных степеней. Она аналогична программе NAry, но
реализует представление на основе массивов. Если вы посмотрите на код програм-
мы FStar, то увидите, насколько сложно в ней добавлять и удалять узлы. Следую-
щий код показывает, каким образом удаляется узел.
// Удаление выделенного узла из дерева.
// У узла не должно быть дочерних.
procedure TFStarTree.RemoveSelected;
var
i, first_link, last._link : Integer;
parent_node, parent_link : Integer;
begin
// Нахождение родительского узла.
parent_node := Node^[Selected].Parent;
first_link := Node^[parent_node].FirstLink;
last_link := Node^[parent_node+l].FirstLink-1;
for parent_link := first_link to last_link do
if (ToNode^[parent_link]=Selected) then break;
// Если родительский узел найден, удаляем его.
if (parent_link<=last_link) then
begin
// Заполнение пустого места в массиве ToNode.
for i := parent_link to NumLinks-1 do
ToNode^[i] := ToNode^[i+1] ;
NumLinks := NumLinks-1; .
// He стоит изменять размеры массива ToNode.
// Обновление записей массива FirstLink.
for i : = 1 to NumNodes do
if (Node^[i].FirstLink>parent_link) then
Node^[i].FirstLink := Node^[i].FirstLink-1;
end;
// Удаление самого узла заполнением пустого места в массиве ToNode.
for i := Selected to NumNodes-1 do
Node^[i] := Node^[i+l] ;
NumNodes := NumNodes-1;
// Обновление записей массива ToNode.
for i := 1 to NumLinks do
if (ToNode'4 [i] >Selected) then
ToNode^[i] := ToNode^[i] -1;
Selected := 0;
end;
Этот код гораздо сложнее, чем соответствующий код программы NAry, исполь-
зующийся для изменения узла с массивом указателей на потомков.
// Удаление дочернего узла.
procedure TNAryNode.RemoveChild(target : TNAryNode);
var
num, I : Integer;
begin
// Нахождение дочернего узла.
for num := 1 to NumChildren do
begin
if (Children^[num] = target) then break;
end;
if (num>NumChildren) then
raise EInvalidOperation.Create(
'Удаляемый узел не является дочерним узлом найденного родителя.');
// Освобождение памяти, занимаемой дочерним узлом.
Children^[num].Free;
// Сдвиг оставшихся дочерних узлов для заполнения пустого места.
for i := num+1 to NumChildren do
Children^[i-1] := Children^[i];
Children^[NumChildren] := nil;
NumChildren := NumChildren-1;
end;
|