Аргументы Т, Т1 и Т2 обозначают деревья, представляемые в виде термов, записываемых с помощью тернарного функтора tree (левое поддерево, правое поддерево, метка) и константы nil, например:
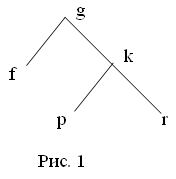
tree (tree (nil, nil, f), tree (tree(nil, nil, p), tree (nil, nil, r), k))
представляет дерево, изображенное на рис.1. В вершинах дерева могут находиться объекты произвольного скалярного типа (в приведенном примере - символы).
12. tree_depth (Т, N): N - глубина дерева (т.е. количество ребер в самой длинной ветви дерева);
13. sub_tree (Т1, Т2): дерево Т1 является непустым поддеревом дерева Т2;
14. flatten_tree (Т, L): L - список меток всех узлов дерева Т («выровненное» дерево);
15. substitute (Т1, V, Т, Т2): Т2 - дерево, полученное путем замены всех вхождений V в дереве Т1 на терм Т.
Исходный код:
domains
t=nil;tree(t,t,string)
slist=string*
predicates
tree_depth(t,integer).
sub_tree(t,t).
flattern_tree(t,slist).
append(slist,slist,slist).
substitute(t,string,string,t).
clauses
%tree_depth
tree_depth(nil,0).%glubina pustogo dereva ravna 0
tree_depth(tree(Left,Right,_),D):-tree_depth(Left,L),tree_depth(Right,R),L>=R,!,D=L+1.
%nahodim glubinu levogo i pravogo poddereva. Esli glubina levogo poddereva bolshe, to otvetom budet ona+1
tree_depth(tree(_,Right,_),D):-tree_depth(Right,R),D=R+1.
%esli ze ne bolshe (a iz-za otsecheniya mi popadaem v tretie pravilo tolko v etom sluchae),
%to otvetom budet glubina pravogo poddereva + 1
%sub_tre
sub_tree(T,T).%esli podderevo ravno tekushemu derevu, to rezultat polozitelnii
sub_tree(S,tree(L,R,_)):-sub_tree(S,L);sub_tree(S,R). %esli derevo yavlyaetsya podderevom
%levogo ili pravogo poddereva, to ono yavlyaetsya podderevom i vsego dereva
%vspomogatelnii predicat append
append([],B,B). %esli pervii spisok pustoi, to rezultat - vtoroi spisok
append([H|Tail],B,[H|NewTail]):-append(Tail,B,NewTail). %esli ne pustoi, to rekursivno soedinyaem
%hvost pervogo spiska so vtorim spiskom i poluchaem tem samim hvost itogovogo spiska
%flattern_tree
flattern_tree(nil,[]).%esli derevo pusto, to otvetom budet pustoi spisok
flattern_tree(tree(Left,Right,S),Ans):-flattern_tree(Left,L),flattern_tree(Right,R),append([S|L],R,Ans).
%inache nahodim spisok vershin levogo i pravogo poddereviev, slivaem ih vmeste, ne zabivaya pro tekushuyu vershinu
%substitute
substitute(nil,_,_,nil).%esli derevo pusto, to kakie bi elementi nas ne interesovali, otvetom budet nil
substitute(tree(Left,Right,V),V,N,tree(NLeft,NRight,N)):-!,substitute(Left,V,N,NLeft),substitute(Right,V,N,NRight).
%esli tekushaya vershina ravna iskomoi, to rekursivno zamenyaem levoe i pravoe podereviya, i menyaem tekushuyu vershinu
substitute(tree(Left,Right,X),V,N,tree(NLeft,NRight,X)):-substitute(Left,V,N,NLeft),substitute(Right,V,N,NRight).
%inache (iz-za otsecheniya syuda popadaem tolko esli tekushii element ne raven iskomomu)rekursivno zamenyaem podderevya
goal
tree_depth(tree(tree(nil,nil,f),tree(tree(nil,nil,p),tree(nil,nil,r),k),g),D),write(D),nl,nl,nl,
sub_tree(tree(tree(nil,nil,p),tree(nil,nil,r),k),tree(tree(nil,nil,f),tree(tree(nil,nil,p),tree(nil,nil,r),k),g)),
flattern_tree(tree(tree(nil,nil,f),tree(tree(nil,nil,p),tree(nil,nil,r),k),g),F),write(F),nl,nl,nl,
substitute(tree(tree(nil,nil,f),tree(tree(nil,nil,p),tree(nil,nil,r),k),g),r,a,Ans),write(Ans),nl,nl,nl.
|