Теоретические сведения. Для модели M обычно требуется выполнение не-
которого свойства. В частности, пусть объект F построен, самое боль-
шее, из свободных переменных x0, . . . , xn−1 - с помощью способов ком-
бинирования. Помимо именно этих свободных переменных в F не могут
входить никакие другие свободные переменные. Тогда комбинаторная пол-
нота моделиM понимается как существование в ней такого объекта (кон-
цепта) f, что для всяких переменных x0, . . . , xn−1 справедливо суждение
fx0 . . . xn−1 = F. Другими словами, в модели в явном виде существует
как объект самостоятельный концепт f, реализующий ту же самую смы-
словую нагрузку, что и F-комбинация других объектов (с ограничением на
использование свободных переменных).
На практике часто используются модели, в которых из равенства
функций f и g, вычисленных на произвольном аргументе d, следует равен-
ство самих функций как объектов:

где по соглашению полагают f d = (f d) и gd = (gd). Такие модели называ-
ются экстенсиональными (ext).
Для аппликативных структур справедлива более сильная форма ком-
бинаторной полноты: существует тот единственный концепт f, что для
всяких свободных в F переменных fx0 . . . xn−1 = F(x0, . . . , xn−1):
If.∀x0 . . .∀xn−1(fx0 . . . xn−1 = F(x0, . . . , xn−1)).
В этой записи символ “I” использован как сокращение для “тот един-
ственный . . . , что . . . ”. Это, фактически, принцип свертывания: ком-
бинация объектов F, среди которых в качестве свободных переменных
использованы только лишь x0, . . . , xn−1, сворачивается до единственного
объекта (концепта) f со всеми теми и только теми свойствами, которые
присущи комбинации F(x0, . . . , xn−1). Это выполняется только для экс-
тенсиональных аппликативных структур и позволяет от сложной фор-
мы записи переходить к анализу единственного объекта, снижая громозд-
кость в рассуждениях.
Задача 4.1 Доказать требуемое равенство.
Формулировка задачи. Доказать, что равенство
λxy.xy = λx.x (η)
выводимо в η − ξ-исчислении λ-конверсии (знак “=” представляет
собой отношение конвертируемости).
Решение.
η--1. Приведем применяемые постулаты:
λx.bx = b, где x не имеет свободных вхождений в b, (η)
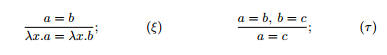
η--2. Применяя эти постулаты, получим:
(1) λxy.xy = λx.(λy.xy), ( по определению)
(2) λy.xy = x, ( по схеме (η))
(3) λx.(λy.xy) = λx.x, ( по схеме (ξ))
(4) λxy.xy = λx.x. ( по схеме (τ))
Приведем сокращенную форму изложения доказательства:
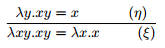 |