Теоретические сведения. Как известно, одним из основных первичных ма-
тематических понятий является понятие числа. Пользуясь числами, стро-
ят другие объекты, более близко представляющие содержательные поня-
тия предметной области. В теоретических исследованиях “хорошим то-
ном” считается свести построенную теорию к какой-либо заранее задан-
ной арифметической системе.
Возникает вопрос, так ли уж неизбежно использовать в качестве пер-
вичного объекта понятие числа. Это один из самых сложных вопросов
современной математики, попытки получения ответа на который приво-
дят к далеко идущим последствиям.
Тем не менее при построении комбинаторной логики илиλ- исчисления
среди исходных объектов нет чисел. Нет ли в этих системах недостатка
в выразительных возможностях ? Оказывается, что в рамках комбина-
торной логики или λ-исчисления можно установить такие комбинаторы
или, соответственно, термы, которые ведут себя как числа. Эти пред-
ставления чисел получили название нумералов. Нумералы как комбинато-
ры удовлетворяют всем законам комбинаторной логики. Более того, мож-
но указать комбинаторы, представляющие арифметические операции, на-
пример, сложение чисел. Исследования в этой области пока все еще далеки
от завершения.
Задача 5.1 Определить объекты, обладающие свойствами натураль-
ных чисел (нумералов) и исследовать их свойства.
Формулировка задачи. Нумералы - это следующие объекты: n¯ =
λxy.(xn)y , где n - натуральное число из множества {1,2,3, . . . }.
Показать, что нумералы это объекты с характеристикой:

Решение.
n¯--1. Форма записи xny определяется по индукции:
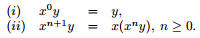
Таким образом, x4y = x(x(x(xy))).
n¯--2. Проверим поведение объектов n¯ = (SB)n(KI) для n = 0,1.
¯0 = (SB)0(KI) = KI, ¯0ab = KIab = Ib = b = (λxy.y)ab, ¯1 = SB(KI), ¯1ab = SB(KI)ab = Ba(KIa)b = BaIb
= a(Ib) = ab = (λxy.xy)ab.
n¯--3. Проверим поведение n¯ = (SB)n(KI) в общем случае.
nab ¯ = (SB)n(KI)ab = SB((SB)n−1(KI))ab ( по определению)
= Ba((SB)n−1(KI)a)b ( по схеме (S))
= a((SB)n−1(KI)ab) ( по схеме (B))
= a(n−1ab) ( по определению)
= a(an−1b) ( по определению)
= anb = (λxy.xny)ab. ( по определению)
Ответ. Нумералы (λxy.xny) имеют вид (SB)n(KI).
Задача 5.2 Определить объект, представляющий операцию “+1”
на множестве нумералов и исследовать его свойства.
Формулировка задачи. Показать, чтоσ = λxyz.xy(yz)задает на мно-
жестве нумералов функцию “следования за” (“прибавление едини-
цы”):

Решение.
σ--1. Комбинаторная характеристика нумералов: nab ¯ = anb.
σ--2. Применим функцию σ к нумералу n¯ в общем виде:
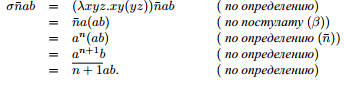
Итак, σnab ¯ = n+ 1ab, то есть σn¯ = n+ 1.
Ответ. Функция σ = λxyz.xy(yz) есть функция следования для нумералов n¯ = λxy.xny.
Задача 5.3 Определить объект, вычисляющий длину конечной последовательности (списка)
Формулировка задачи. Показать, что функция
Length = λxy.Null x ¯0(σ(Length(Cdr x))y).
есть функция определения длины списка x :
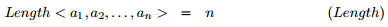
Решение.
Length--1. Введем вспомогательные функции Null и Cdr :

Length--2. ПриложимLength к пустому списку N il:

Таким образом, функция Length корректна по отношению к
применению к пустому списку, то есть Length N il = ¯0.
Length--3. Приложим функцию Lengthк списку x, состоящему из
одного элемента: x =< a >:

Функция Length корректна по отношению к применению к
списку, состоящему из одного элемента, то есть равна ¯1.
Length--4. Теперь проверимLength в общем случае 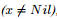 , где , где
знак  означает “не конвертируется к”: означает “не конвертируется к”:

Ответ. ФункцияLength действительно вычисляет длину списка. |