Постановка задачи.
Интервалы прихода клиентов в парикмахерскую с одним креслом распределены равномерно: 18÷6 мин. Время стрижки также распределено равномерно: 16÷4 мин. Клиенты приходят в парикмахерскую, стригутся в порядке «первым пришел — первым обслужен» и затем уходят. Модель парикмахерской на GPSS должна обеспечить сбор статистических данных об очереди. Необходимо промоделировать работу в течение 8 часов модельного времени.
Графическое представление модели
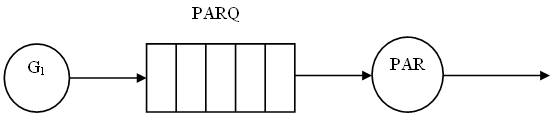
Листинг программы
; первый сегмент программы
10 GENERATE 18,6 ; приход клиентов
20 QUEUE PARQ ; присоединение к очереди
30 SEIZE PAR ; переход в кресло парикмахера
40 DEPART PARQ ; уход из очереди
50 ADVANCE 16,4 ; обслуживание у парикмахера
60 RELEASE PAR ; освобождение парикмахера
70 TERMINATE ; уход из парикмахерской
; второй сегмент программы
80 GENERATE 480 ; транзакт приходит в момент времени, равный 480
90 TERMINATE 1 ; завершение моделирования
Результаты моделирования

Анализ результатов
Прибор
1. Парикмахер был занят обслуживанием 27 раз, ENTRIES (число входов)=27.
2. Он был занят в течение 88.5% времени, UTIL. (загрузка)=0.885.
3. Среднее время интервала обслуживания парикмахера равно 15,74 мин, AVE_TIME (среднее время)=15.74.
4. После окончания интервала времени, равного 8 ч, в кресле остался один необслуженный клиент, AVAILABLE=1.
Очередь
1. В очереди к парикмахеру никогда не было более одного клиента, MAX (максимальное содержимое)=1.
2. Содержимое очереди на момент окончания моделирования равно 0, CONT. (содержимое)=0.
3. Всего в очередь входило 27 клиентов, ENTRIES (число входов)=27.
4. Среди этих 27 входов было 8 нулевых, ENTRIES(0) (число нулевых входов)=8.
5. Среднее число клиентов, находившихся в очереди, равно 0,23, AVE_CONT (среднее содержимое)=0.23.
6. Среднее время пребывания клиентов в очереди равно 4.11, AVE_TIME (среднее время) =4.11.
7. Среднее время пребывания клиентов в очереди (исключая нулевые входы) равно 5.84, AVE(-0) (среднее время, исключая нулевые входы) =5.84.
|