Удаление элемента из сортированного дерева немного сложнее, чем добавле-
ние. После этой операции программа должна перестроить другие узлы, чтобы со-
хранить в дереве соотношение «меньше чем». Следует рассмотреть несколько су-
ществующих вариантов.
Во-первых, если удаляемый узел не имеет потомков, допустимо просто убрать
его из дерева. При этом порядок остальных узлов не изменяется.
Во-вторых, если удаляемый узел имеет один дочерний узел, можно заменить
его дочерним узлом. При этом порядок потомков данного узла остается тем же,
так как эти узлы также являются и потомками дочернего узла. На рис. 6.17 показа-
но дерево, где удаляется узел 4, имеющий только один дочерний узел.
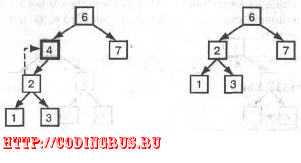
Рис. 6.17. Удаление узла с единственным потомком
Если удаляемый узел имеет два дочерних, вовсе не обязательно, что один из них
займет его место. Если потомки узла также имеют по два дочерних, то для размеще-
ния всех дочерних узлов в позиции удаленного узла просто нет места. У удаленного
узла есть один лишний потомок, а дочерний узел, которым вы могли бы заменить
исходный, имеет два дочерних узла, поэтому вы должны объявить три дочерних
записи узла в данной позиции.
Чтобы решить эту проблему, вы должны заменить удаленный узел крайним
правым узлом дерева из левой ветви. Другими словами, двигайтесь вниз от уда-
ленного узла по левой ветви. Затем двигайтесь вниз по правым ветвям до тех пор,
пока не найдете узел без правой ветви. Это и есть нужный узел. В дереве, изобра-
женном слева на рис. 6.18, нужный узел - крайний правый на ветви слева от узла 4.
Вы можете заменить узел 4 узлом 3 и сохранить порядок следования элементов
дерева.
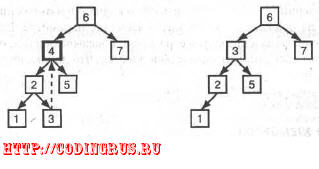
Рис. 6.18. Удаление узла с двумя потомками
Остается последний вариант - когда заменяющий узел имеет левого потомка.
В этом случае вы можете переместить данного потомка в позицию, освобожден-
ную в результате перемещения узла, и дерево снова будет упорядочено. Крайний
правый узел не имеет правого дочернего узла, иначе он не являлся бы таковым.
Следовательно, не нужно беспокоиться, сколько потомков имеет замещающий
узел.
На рис. 6.19 проиллюстрирована эта сложная ситуация. В данном примере
удаляется узел 8. Крайний правый узел слева - узел 7, который имеет дочерний
узел 5. Чтобы удалить узел 8, сохранив порядок элементов дерева, замените узел 8
узлом 7, а узел 7 - узлом 5.
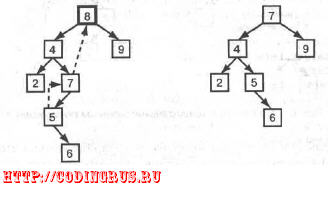
Рис. 6.19. Удаление узла, если замещающий его узел имеет дочерние
Обратите внимание, что узел 7 получает абсолютно новые дочерние записи,
а узел 5 остается с одним дочерним узлом.
При помощи следующего кода удаляется узел из сортированного двоичного дерева:
// Удаление элемента ниже выделенного узла.
procedure TSortTree.RemoveNode(var node : TSortNode;
target_value : Integer);
var
target : TSortNode;
begin
// Если элемент не найден, вывести сообщение.
if (node = nil) then
begin
ShowMessage(Format('Элемент %d не является узлом дерева.'
,[target^value]));
expend;
if (target_value
.// Продолжаем с левым нижним поддеревом.
RemoveNode(node.LeftChild,target_value)
else if (target_value>node.Id) then
// Продолжаем с правым нижним поддеревом.
RemoveNode(node.RightChiId,target_value)
else begin
// Это искомый элемент.
if (node.LeftChild = nil) then
begin
// Если у элемента нет левого дочернего узла,
// перемещаем его с правым дочерним.
target := node;
node := node.RightChiId;
target.RightChild := nil;
target.Free;
end else if (node.RightChild = nil) then
begin
// Если у элемента нет правого дочернего узла,
// перемещаем его с левым дочерним.
target := node;
node := node.LeftChild;
target.LeftChild := nil;
target.Free;
end else begin
// Если элемент имеет два дочерних узла,
// используем ReplaceRightmost для замены элемента
// его крайним правым потомком слева.
ReplaceRightmost(node,node.LeftChild);
end; // Конец замены элемента.
end; // Конец if левый ... else if правый ... else ...
end;
// Заменяем элемент его крайним правым потомком слева.
procedure TSortTree.ReplaceRightmost(var target, repL : TSortNode);
var
old_repl, tmp : TSortNode;
begin
if (repl.RightChildonil) Then
begin
// Сдвигаем родительский узел вниз вправо.
ReplaceRightmost(target,repl.RightChild);
end else begin
// Достигли конца дерева. Запоминаем узел repl.
old_repl : = repl ;
// Заменяем repl левым дочерним узлом.
repl := repl.LeftChild;
// Заменяем нужный элемент repl.
old_repl.LeftChild := target.LeftChild;
old_repl.RightChild := target.RightChild;
tmp := target;
target := old_repl;
tmp.LeftChild := nil;
tmp.RightChild := nil;
tmp.Free;
end;
end;
В этом алгоритме дважды применяется способ передачи параметров в рекур-
сивные процедуры по ссылке. Сначала процедура RemoveNode использует этот
способ, чтобы родительский узел удаляемого элемента указывал на заменяющий
узел. Следующая команда показывает, как вызывается процедура RemoveNode:
RemoveNode(node.LeftChild,target_value)
Когда процедура находит искомый узел (узел 8 на рис. 6.19), она получает в ка-
честве параметра узла node указатель родителя на искомый узел. Установив этот
параметр для замещающего узла (узел 7), процедура Deleteltem задает дочерний
узел для родителя так, чтобы он указывал на новый узел.
Следующая команда показывает, как процедура ReplaceRightmost рекур-
сивно вызывает себя:
ReplaceRightmost(target,repl.RightChild);
Когда эта процедура находит самый правый узел в левой от удаляемого узла
ветви (7-й), параметр repl сохраняет указатель родительского узла на крайний
правый узел. Когда процедура устанавливает значение repl в repl. LeftChild,
она автоматически соединяет родителя крайнего правого узла с левым потомком
крайнего правого узла (узел 5).
Программа TrSort использует эти процедуры для управления сортированны-
ми двоичными деревьями. Введите целое число и нажмите кнопку Add, чтобы доба-
вить элемент к дереву. Введите целое число и щелкните по кнопке Remove, чтобы
удалить элемент. После этого дерево автоматически перестраивается, чтобы со-
хранить порядок . |