Описание метода выбора наилучшей многомерной альтернативы, состоящей в решении соответствующих оптимизационных задач.
Пусть для каждого частного критерия Kv можно указать пороговое значение Lv такое что альтернативы, оценки которых по критерию Kv ниже, чем Lv, крайне не желательны. Более предпочтительными считаются альтернативы, оценки которых по частным критериям как можно дальше отстоят от критических значений Lv. Формализуем это предположение. Пусть альтернативы A={a1,..,an} оцениваются по s частным критериям K1,..Ks и Xi1,..,Xis – оценки альтернативы ai, i принадлежит {1,..,n}. Альтернативу ai будем считать более предпочтительной, чем aj, если:
Min{Xi1-L1,..,Xis-Ls} > min{Xj1-L1,..,Xjs-Ls}.
Тогда выбор наилучшей альтернативы осуществляется как решение задачи отыскания максимума выражения:
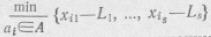 (4.26) (4.26)
Решение этой задачи эквивалентно решению следующей задачи линейного программирования:
z->max (4.27)
при ограничениях:
Xiv-Lv-z >= 0, v принадлежит {1,..,s}. (4.28)
ai принадлежит A (4.29)
Если число альтернатив невелико, то задача может быть решена непосредственным расчетом значений (4.26) и выбором альтернативы имеющей максимальное значение. Если z<0, то не существует среди А альтернативы, все оценки которой выше критических значений.
|