Как и переменные, функции не связаны с определенными блоками.
Существует пять типов функций:11 1) непрерывные числовые значения Сn; 2) дискретные
числовые значения Dn; 3) перечень числовых значений Ln; 4) дискретные значения
атрибутов Еn; 5) перечень значений атрибутов Мn. Первые два типа функции, являются
основными. На рис. 5 показана непрерывная функция.
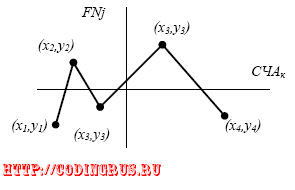
Рис. 5. Непрерывная функция GPSS
Каждая функция определяется посредством карты, имеющей вид
Метка Операция A B
j FUNCTION Arg Cn
В поле А определяется аргумент функции Arg, который может быть СЧА. В поле В
указываются тип функции и число точек, для которых вычисляется функция,
Каждая карта FUNCTION сопровождается картами, содержащими значения отдельных
точек функции (пары Xi и Yi). Каждая из этих карт может содержать шесть пар Xi и Yi),
расположенных на 12 шестисимвольных полях. Например, функцию, показанную на рис. 5, можно представить следующим образом:
Метка Операция
1 FUNCTION RN1,C5
X1,Y1/X2,Y2/X3,Y3/X4,Y4/X5,Y5
Значения Xi и Yi могут быть нецелыми числами. Значения Х должны удовлетворять
условию Xi < Xi+1.
Пользователь может представить координаты функции в свободном формате, а не по
шесть на каждой карте. Для этого нужно, чтобы: 1) первое число начиналось с колонки 1;
2) последнее число кончалось до или в 71-й колонке; 3) координаты Xi и Yi отделялись
друг от друга запятой; 4) пары координат отделялись друг от друга знаком «/».
Например, если необходимо, чтобы случайная величина получала значения 1, 4, 5 с
относительной частотой 0,40; 0,10; 0,50, то дискретная функция может иметь вид
15 FUNCTION RN8,D3
0.4,1/.5,4/1,5
Графическое представление данной функции приведено на рис. 6
У функции аргументом может необязательно RNj. Например, аргументом может быть
любой СЧА. При использовании аргументов, отличных от RNj, существуют ограничения:
1. Значениями аргумента должны быть только целые числа;
2. Когда значение аргумента выходит за пределы, указанные в описании функции, то
значение последней берется равным ближайшим описанным значениям.
Генерация случайных чисел в GPSS имеет следующие особенности. Все случайные
равномерно распределенные числа, используемые в GPSS, получаются в результате
расчета, который исходит из набора восьми основных чисел, называемых исходными.
Пользователь может задать любое из этих чисел (RN1, ...,RN8). В случаях, когда
обращение к датчику случайных чисел подразумевается, используется RNj. Начальные
значения и, следовательно, последовательности псевдослучайных чисел, получаемые во
всех системных датчиках (RN1, .,.,RN8), одинаковы. Для получения различных
последовательностей необходимо изменять их начальное значение.
 Моделирование Моделирование
пуассоновских потоков в GPSS.
Наступление событий часто
подчиняется следующим
условиям:
1. Вероятность того, что
наступление события
возникает на некотором
интервале,
пропорционально длине
этого интервала.
2. Вероятность того, что
возникнут два и более
событий в течение
малого промежутка времени, пренебрежимо мала (ординарный процесс).
3. Все интервалы наступления независимы друг от друга (процесс с ограниченным
последействием)
Для указанных условий выведена зависимость (закон Пауссона), характеризующая
скорость наступления событий
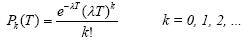
где Pk(T) – вероятность того, что ровно k событий произойдет за время T; λ - средняя
интенсивность наступления событий. Когда интенсивность наступления распределена по
закону Пауссона, соответствующие значения интервалов времени наступления
распределены по экспоненциальному закону: ИВН = ИВНср⋅[-ln(1-RNi)], где ИВНср –
средний интервал времени наступления, RNi – случайное число (RNi ∈[0, 1]). Знак минус
принят в выражении потому, что значение логарифма отрицательно. Вычисление
натурального логарифма в GPSS не предусмотрено и выражение -ln(1-RNi)
аппроксимируется ломаной прямой, заданной координатами 24 точек
EXPON FUNCTION RN1,C24
0,0/.100,.104/.200,.222/.300,.355/.400,.509/.500,.690
.600,.915/.700,1.200/.750,1.380/.800,1.600/.840,1.830/.880,2.120
.900,2.300/.920,2.520/.940,2.810/.950,2.990/.960,3.200/.970,3.500
.980,3.900/.990,4.600/.995,5.300/.998,6.200/.999,7/1,8
График функции EXPON показан на рис. 7.
Например, необходимо смоделировать пуассоновский входящий поток со средним
значением 6 заявки в течение каждых 24 часов. Единица измерения – 1 мин. В таком
случае блок GENERATE будет иметь вид
GENERATE 240,FN$EXPON
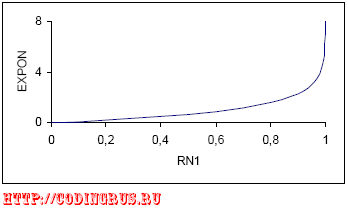
Рис. 7
Операнд A получен путем преобразования интенсивности в соответствующее ей
среднее время между последовательными поступлениями заявок: 4 часа или 240 мин.
Например, если значение RNj равно 0,55, значение функции FN$EXPON будет равно
0,8025. Произведение 0,8025⋅240 равно 192,6. Следовательно, следующая заявка поступит
в модель через 192 мин. Так как, для пуассоновского потока принято предположение, что
интервал между двумя последовательными поступлениями не может равен нулю, то
рекомендуется значение операнда A блока GENERATE брать не менее 50.
В GPSS предусмотрен сбор и обработка типовых статистических данных по
каждому объекту (максимальная и средняя длина очереди, коэффициент загрузки
устpойства, памяти, сpеднее вpемя обpаботки в устройстве и ожидания в очеpеди и дp.), а
также дополнительной статистики, заложенной программистом в модели. Процесс
имитации функционирования системы во времени (динамика процесса
функционирования) может быть представлен и в графическом виде, что особенно
эффективно для учебных целей.
В статистической категории GPSS используется два типа объектов: очереди и
таблицы.
Сноски:
11 n – число точек, задающих функцию |