Пусть нам требуется построить алгоритм сортировки, оптимальный по количеству выполняемых при этом операций присваивания или сравнения для худшего случая. Из приведенной выше таблицы следует, что алгоритм прямого выбора является линейным по количеству выполняемых операций присваивания (их количество для худшего случая равно 3(N — 1)) и, следовательно, асимптотически оптимален. Более того, при использовании дополнительного массива для записи результата этот алгоритм можно реализовать ровно за N перемещений элементов, что является точной нижней оценкой для количества присваиваний в худшем случае, а именно — если все N элементов первоначально находились не на своих местах, мы не можем менее, чем за N перемещений, расставить их в нужном порядке. Данное свойство алгоритма прямого выбора можно использовать и в практическом программировании, когда при сортировке некоторых объектов операция присваивания (перемещения) оказывается значительно более трудоемкой, чем операция сравнения. Например, при сортировке столбцов двухмерного массива согласно значениям первых элементов столбцов или при сортировке записей, по значению одного из полей, или при сортировке настоящих контейнеров, которые требуется переставить с помощью подъемного крана по возрастанию стоимости находящихся в них грузов. Справедливости ради заметим, что такую техническую проблему при компьютерной сортировке можно решать и по-другому: сортировать можно не сами объекты, а указатели на них.
На олимпиаде задача построения оптимального по количеству перемещений алгоритма сортировки может быть поставлена и иначе. Например, попробуйте найти оптимальное решение задачи “Парковка”, предлагавшейся на международной олимпиаде по информатике в 2000 году. Учтите, что для каждой из конкретных входных неупорядоченных последовательностей, оно может быть своим. Определите, для любых ли значений N из условия задачи это можно сделать в общем случае. Универсальное решение этой задачи, рассмотренное в [7], является эвристическим и не всегда минимально, хотя и удовлетворяет условию.
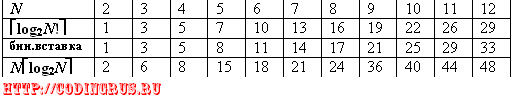
Перейдем теперь к рассмотрению алгоритма сортировки, оптимального по количеству сравнений элементов между собой. Если изначально нам не известны никакие отношения между элементами, то для N элементов результатом их сортировки может оказаться любая из N! перестановок элементов. Тогда из теории информации следует, что нижняя граница числа сравнений, необходимых в худшем случае для определения нужной нам перестановки, равна [log2N!]. При больших N это число растет так же, как и N[log2N] — теоретическая оценка сверху для ряда универсальных алгоритмов (см. таблицу выше). Например, алгоритм вставки на первом шаге сравнивает элементы a1 и a2, на втором — в упорядоченную последовательность из 2-х элементов вставляется элемент a3 и т.д. Если поиск места для вставки очередного элемента в уже упорядоченную последовательность сделать бинарным, то число сравнений в худшем случае составит [log22] + [log23] + … + [log2N] и будет отличаться от [log2N!], менее чем на N. Составим таблицу, в которой для небольших N приведены сравнительные значения результатов вычисления по трем формулам:
Несложно показать, что и другие универсальные алгоритмы сортировки, имеющие ту же асимптотическую оценку на количество сравнений, не совпадают по количеству сравнений с точной нижней оценкой. В задачниках по программированию встречается упражнение, требующее отсортировать 5 произвольных элементов не более, чем за 7 сравнений (убедитесь, что любой универсальный алгоритм сделает это, в худшем случае используя 8 сравнений, и попробуйте самостоятельно построить алгоритм для решения этой задачи, так как это действительно возможно сделать за 7 сравнений).
В [8] показано, как для известного фиксированного значения N за абсолютно минимальное число сравнений отсортировать конкретную входную последовательность из N элементов. Для этого можно использовать так называемый метод центров тяжестей. Пусть некоторое количество сравнений уже было проведено, то есть наше множество элементов частично упорядочено. Назовем линейными продолжениями такого множества те перестановки из N элементов, которые не противоречат уже имеющемуся частичному упорядочению. Тогда a(i) – среднее место i-го элемента из входного массива a в упорядоченном массиве, по имеющейся на настоящий момент информации можно подсчитать так
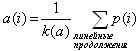
Здесь
p(i)
— место
i-го
элемента в линейном продолжении,
k(a)
- общее число линейных продолжений элементов массива
a.
Два различных элемента
i
и
j
не
сравнимы тогда и только тогда, когда
b(i,
j)
= |a(i)
—
a(j)|
< 1. Более того, в очередном сравнении должны участвовать элементы
i
и
j,
значение
b(i,
j)
у которых минимально и
i
<
j.
После этого количество линейных продолжений уменьшается, средние места элементов
в них пересчитываются и выбирается новая пара элементов для сравнения.
Отсортированный массив соответствует единственному оставшемуся линейному
продолжению, места всех элементов в котором определены, и
b(i,
j)
³
1, если
i
¹
j.
Покажем работу этого
алгоритма на следующем примере. Пусть для 5 элементов уже известно, что
a1
£
a2
£
a3
и a4
£
a5.
Перечислим все 10 линейных продолжений этого множества и подсчитаем среднее
место каждого из 5 элементов в них:
Теперь можно показать в каком
порядке оптимальный по количеству сравнений алгоритм должен сравнивать элементы
изначально никак не упорядоченного массива. До начала сортировки допустимыми
линейными продолжениями являются все
N!
перестановок элементов массива, все элементы в которых равноправны. Так, для 5
элементов все
a(i)
= 3, а
b(i,
j)
= 0. Тогда сначала мы сравниваем два любых элемента, а потом — два любых из
оставшихся, так как значение
b
для них после первого сравнения останется нулевым, то есть минимально возможным.
Подобным образом, выполняются сравнения на первом шаге, например, алгоритма
сортировки слиянием. Пусть теперь известно, что
a1
£
a2
и a4
£
a3.
Очевидно, что
b(1,
4) = b(2,
3) = 0, причем сами значения
a
для упомянутых
элементов можно и не подсчитывать. Таким образом, на третьем шаге мы должны
сравнить, например, максимальные элементы в упорядоченных парах. Пусть окажется,
что a2
£
a3.
Тогда по оставшимся 15 линейным продолжениям легко подсчитать значения
a:
a(1)
= 1,6;
a(2)
= 3,2;
a(3)
= 4,8;
a(4)
= 2,4;
a(5)
= 3. То есть на четвертом шаге, отличном от универсальных сортировок, сравнению
подлежат элементы
a2
и a5.
Вне зависимости от результатов этого сравнения за оставшиеся 3 сравнения массив
будет упорядочен.
Открытым остается вопрос,
всегда ли количество сравнений в таком оптимальном алгоритме совпадает с точной
нижней оценкой для всех алгоритмов сортировки. К сожалению, это не так. Уже при
N
= 12 оптимальному алгоритму потребуется сделать 30 сравнений вместо 29
ожидаемых. Дальнейшее изучение этого вопроса затруднено в силу чрезвычайной
трудоемкости алгоритма, основанного на методе центров тяжестей.
В заключение данного раздела
покажем, как может быть сформулирована олимпиадная задача, в рамках которой
требуется построить алгоритм оптимальный или асимптотически оптимальный по
количеству сравнений.
{задача}
Входным параметром в задаче
является число
N.
После его считывания ваша программа должна выдавать номера элементов, сравнить
которые ей требуется на очередном шаге, и считывать результат этого сравнения.
Когда будет произведено достаточное для вашего алгоритма число сравнений,
программа должна выдать индексы элементов в массиве в порядке неубывания
значений соответствующих элементов.
Вместо диалогового режима
работы может быть предложена специальная библиотечная функция из созданного
специально для этой задачи модуля, путем обращения к которой можно будет
получать информацию о соотношении значений у пары элементов.
|
Главная
Каталог файлов
