Рассмотрим принцип организации семантических сетей. В семантической сети сущности и классы сущностей ассоциируются с узлами, а отношения между сущностями ассоциируются с дугами, соединяющими узлы. Дуга, подсоединенная к единственному узлу, устанавливает свойство этого узла. Семантическая сеть позволяет выполнять вывод но цепочкам, описываемым определенными типами дуг. Например, в сети, изображенной на , узел «мероприятие» обладает свойством «проводится». Узел «собрание» соединен дугой с узлом «мероприятие», поэтому можно прийти к выводу о том, что узел «собрание» также обладает свойством «проводится».
Важнейшей концепцией формализма семантических сетей является иерархия, поэтому данный формализм особенно удобен для представления таксономий знаний. Каждый уровень таксономии представляется в виде узла, который соединен дугами "является" с более высокими и более низкими уровнями. К примеру, на рис. 3.2 «мероприятие» - это наивысший уровень таксономии, а на следующем уровне могут располагаться различные виды мероприятий.
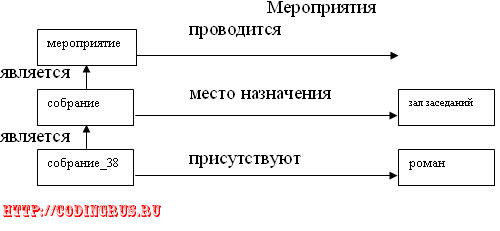
Рис. 3.2
Если рассматривать семантическую сеть как описание отношений, которые поддерживаются между сущностями, то ее можно непосредственно реализовать при помощи языка Пролог. Нижеследующая программа выражает структуру сети с «мероприятиями», представленную на рис. 3.2:
является (собрание, мероприятие).
является (собрание_38, собрание).
присутствуют(роман, собрание_38).
проводится (мероприятие).
проводится (X ) :- является ( X, Y ) , проводится ( Y ).
назначается_в (X,Y) :- является (X, Z), назначается_в (Z, Y).
Вторая фраза "назначается_в" позволяет сделать вывод о том, что «собрание_38» назначается в зале заседаний, так как «собрание_38» - это собрание, а любая сущность, которая является собранием, назначается в зале заседаний. Вывод можно выполнить в любом месте, где два узла диаграммы связаны дугой "является". Дуга "является" представляет либо отношение включения в класс (например, класс собраний включается в класс мероприятий), либо отношение принадлежности к классу («собрание_38» - это член класса собраний). |