Представление в виде И/ИЛИ - графов наиболее хорошо приспособлено для задач, которые естественным образом разбиваются на взаимно независимые подзадачи. Примерами таких задач могут служить поиск маршрута, игровые задачи, доказательство теорем и т.п.
Для некоторых категорий задач представление в форме И/ИЛИ-графа является более естественным. Такое представление основано на разбиении задач на подзадачи. Разбиение на подзадачи дает преимущества в том случае, когда подзадачи взаимно независимы, а, следовательно, и решать их можно независимо друг от друга.
Проиллюстрируем это на примере. Рассмотрим задачу отыскания на карте дорог маршрута между двумя заданными городами, как показано на рис. 3.4. Не будем пока учитывать длину путей. Разумеется, эту задачу можно сформулировать как поиск пути в пространстве состояний. Соответствующее пространство состояний выглядело бы в точности, как карта рис. 3.4: вершины соответствуют городам, дуги - непосредственным связям между городами. Тем не менее давайте построим другое представление, основанное на естественном разбиении этой задачи на подзадачи.
Поиск маршрута из а в z на карте дорог
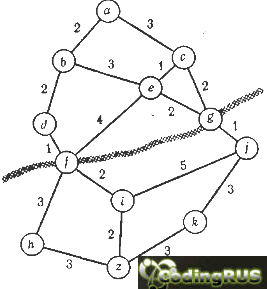
Рис. 3.4.
На карте рис. 3.4 мы видим также реку. Допустим, что переправиться через нее можно только по двум мостам: один расположен в городе f, другой -в городе g. Очевидно, что искомый маршрут обязательно должен проходить через один из мостов, а значит, он должен пройти либо через f, либо через g. Таким образом, мы имеем две главных альтернативы:
Для того, чтобы найти путь из а в г, необходимо найти одно из двух:
(1) путь из а в г, проходящий через f, или
(2) путь из а в г, проходящий через g.
И/ИЛИ-представление задачи поиска маршрута
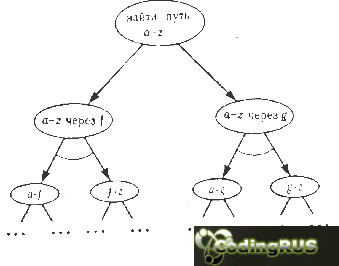
Рис. 3.5.
Теперь каждую из этих двух альтернативных задач можно, в свою очередь, разбить следующим образом:
(1) Для того, чтобы найти путь из а в г через f, необходимо:
1.1 найти путь из а в f и
1.2 найти путь из f в z.
(2) Для того, чтобы найти путь из a в z через g, необходимо:
2.1 найти путь из а в g и
2.2 найти путь из g в z.
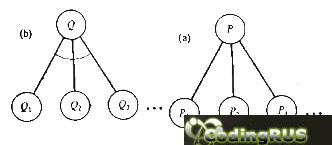
Рис. 3.6.
Итак, мы имеем две главных альтернативы для решения исходной задачи: (1) путь через f или (2) путь через g. Далее, каждую из этих альтернатив можно разбить на подзадачи (1.1 и 1.2 или 2.1 и 2.2 соответственно). Здесь важно то обстоятельство, что каждую из подзадач в обоих альтернативах можно решать независимо от другой. Полученное разбиение исходной задачи можно изобразить в форме И/ИЛИ-графа (рис. 3.5). Обратите внимание на полукруглые дуги, которые указывают на отношение И между соответствующими подзадачами. Граф, показанный на рис. 3.5 - это всего лишь верхняя часть всего И/ИЛИ-дерева. Дальнейшее разбиение подзадач можно было бы строить на основе введения дополнительных промежуточных городов.
Какие вершины И/ИЛИ-графа являются целевыми? Целевые вершины - это тривиальные, или «примитивные» задачи. В нашем примере такой подзадачей можно было бы считать подзадачу «найти путь из а в с», поскольку между городами а и с на карте имеется непосредственная связь.
Рассматривая наш пример, мы ввели ряд важных понятий. И/ИЛИ-граф - это направленный граф, вершины которого соответствуют задачам, а дуги отношениям между задачами. Между дугами также существуют свои отношения. Это отношения И и ИЛИ, в зависимости от того, должны ли мы решить только одну из задач-преемников или же несколько из них (см. рис. 3.6). В принципе из вершины могут выходить дуги, находящиеся в отношении И вместе с дугами, находящимися в отношении ИЛИ. Тем не менее, мы будем предполагать, что каждая вершина имеет либо только И-преемников, либо только ИЛИ-преемников; дело в том, что в такую форму можно преобразовать любой И/ИЛИ-граф, вводя в него при необходимости вспомогательные ИЛИ-вершины. Вершину, из которой выходят только И-дуги, называют И-вершиной; вершину, из которой выходят только ИЛИ-дуги, - ИЛИ-вершиной.
Что же является решением в случае И/ИЛИ-представления? Решение должно, конечно, включать в себя все подзадачи И-вершины. Следовательно, это уже не путь, а дерево. Такое решающее дерево Т определяется следующим образом:
• исходная задача Р - это корень дерева Т;
• если Р является ИЛИ-вершиной, то в Т содержится только один из ее преемников (из И/ИЛИ-графа) вместе со своим собственным решающим деревом;
• если Р - это И-вершина, то все ее преемники (из И/ИЛИ-графа) вместе со своими решающими деревьями содержатся в Т.
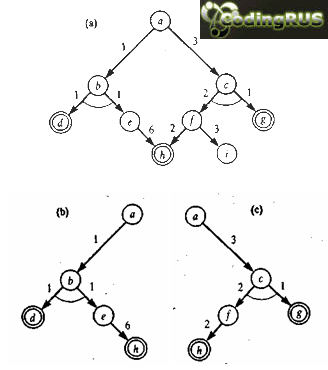
Рис. 3.7
Иллюстрацией к этому определению может служить рис. 3.7. Используя стоимости, мы можем формулировать критерии оптимальности решения. Например, можно определить стоимость решающего графа как сумму стоимостей всех входящих в него дуг. Тогда, поскольку обычно мы заинтересованы в минимизации стоимости, мы отдадим предпочтение решающему графу, изображенному на рис. 3.7(с).
Для задачи отыскания кратчайшего маршрута (рис. 3.4) И/ИЛИ-граф вместе с функцией стоимости можно определить следующим образом:
• ИЛИ-вершины представляются в форме X-Z, что означает: найти кратчайший путь из X в Z.
• И-вершины имеют вид X-Z через Y , что означает: найти кратчайший путь из X в Z, проходящий через Y.
• Вершина X-Z является целевой вершиной (примитивной задачей), если на карте существует непосредственная связь между X и Z.
• Стоимость каждой целевой вершины X-Z равна расстоянию, которое необходимо преодолеть по дороге, соединяющей X с Z.
• Стоимость всех остальных (нетерминальных) вершин равна 0.
В этом разделе нас будет интересовать какое-нибудь решение задачи независимо от его стоимости, поэтому проигнорируем пока стоимости связей или вершин И/ИЛИ-графа. Простейший способ организовать поиск в И/ИЛИ-графах средствами Пролога - это использовать переборный механизм, заложенный в самой пролог-системе. Оказывается, что это очень просто сделать, потому что процедурный смысл Пролога это и есть не что иное, как поиск в И/ИЛИ-графе. Например, И/ИЛИ-граф рис. 3.7 (без учета стоимостей дуг) можно описать при помощи следующих предложений:
a :- b. % а - ИЛИ-вершина с двумя преемниками
a :- c. % b и с
b :- d, е. % b - И-вершина с двумя преемниками d и е
c :- h.
c :- f, g.
f :- h, i.
d. g. h. % d, g и h - целевые вершины
Для того, чтобы узнать, имеет ли эта задача решение, нужно просто спросить:
?- а.
Получив этот вопрос, пролог - система произведет поиск в глубину в дереве рис. 3.7 и после того, как пройдет через все вершины подграфа, соответствующего решающему дереву рис. 3.7(b), ответит «да». |