Граф может быть представлен либо явно - в виде одной структуры, либо неявно - набором фактов вида edge (P, R, N), устанавливающих наличие ребра (дуги) между вершинами (узлами) P и R и стоимость N (целое неотрицательное число) этого ребра. При явном способе задания графа он представляется термом, включающим в свой состав список ребер (заданных аналогично с помощью тернарного функтора edge) и, возможно, список вершин графа.
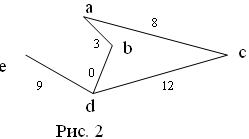
Граф, изображенный на рисунке 2, может быть задан неявно фактами edge(a, c, 8), edge(a, b, 3), edge(c, d, 12), edge(b, d, 0), edge(e, d, 9), а в явной форме - например, термом graph([edge(a, c, 8), edge(a, b, 3), edge(c, d, 12), edge(b, d, 0), edge(e, d, 9)], [a, b, c, d, e]), где graph - бинарный фунтор.
В нижеследующем описании предикатов используется первый (неявный) способ задания графа, Х и У обозначают вершины графа, а L - список вершин.
16. path (Х, У, L): L - путь без петель между вершинами Х и У, т.е. список вершин между этими вершинами;
17. min_path (Х, У, L): L - путь между вершинами Х и У, имеющий минимальную стоимость (стоимость пути равна сумме стоимостей входящих в него ребер);
18. short_path (Х, У, L): L - самый короткий путь между вершинами Х и У (длина пути равна количеству ребер, входящих в него);
19. cyclic : граф является циклическим (т.е. не является деревом);
20. is_connected : граф является связным (т.е. для любых двух его вершин существует связывающий их путь).
Замечания:
1) В предикатах 16-19 граф предполагается связным и может содержать циклы;
2) Все вышеописанные предикаты группы IV для второго способа представления графа должны содержать дополнительный аргумент - сам граф, например: path (G, X, Y, L), где G - структура, представляющая граф.
Исходный код программы:
%k poisku kommentarii net, eto slozno obyasnit, pochitaite knigu Soshnikova "Paradigma logicheskogo programmirovaniya"
domains
slist=string*
l=slist*
way=w(integer,slist)%dlya hraneniya puti. Hranit summarnuyu stoimost puti i sam put
wlist=way*
predicates
edge(string,string,integer).
e(string,string,integer).
path(string,string,slist).
p(string,slist,slist).
member(string,slist).
min_path(string,string,slist).
prolong(way,way).
place(wlist,wlist,wlist).
placeone(way,wlist,wlist).
ucs(string,wlist,way).
short_path(string,string,slist).
weight(string,l,slist).
n(slist,slist).
append(l,l,l).
lenght(slist,integer).
cyclic.
q(slist,integer).
is_connected.
not_connected.
clauses
edge(a,c,8).
edge(a, b, 3).
edge(c, d, 12).
edge(b, d, 0).
edge(e, d, 9).
e(A,B,C):-edge(A,B,C);edge(B,A,C). %budem schitat, chto graf nenapravlenii
%vspomogatelnii predikat member(E,L), proveryayushii prinadlezit li element E spisku L
member(H,[H|_]). %esli element raven golove spiska, to rezultat polozitelnii
member(X,[_|Tail]):-member(X,Tail). %esli element vstrechaetsya v hvoste spiska, to rezultat polozitelnii
%path
%mozno pochitat v knige pro poisk v glubinu na str 159
path(A,B,P):-p(A,[B],P).%ishem put ot konechnoi vershini v nachalnuyu. Ishodnii put budet sostoyat iz odnoi konechnoi vershini
p(A,[A|Tail],[A|Tail]).%esli tekushaya vershina v nashem puti ravna nachalnoi, to etot put yavlyaetsya iskomim
p(A,[B|Tail],P):-e(B,C,_),not(member(C,Tail)),p(A,[C,B|Tail],P). %B-tekushaya vershina puti.
%Nahodim vershinu, v kotoruyu mi mozem popasti iz B, i kotoraya eshe ne vstrecalas v puti,
%i probuem naiti put ot etoi novoi vershini do punkta A
%min_path
%tut slozno opisat, chitaite knigu na str 175
min_path(A,B,P):-ucs(A,[w(0,[B])],w(_,P)).
ucs(A,[w(C,[A|Tail])|_],w(C,[A|Tail])):-!.
ucs(A,[Path|Tail],R):-findall(Z,prolong(Path,Z),NewPathes),!,place(NewPathes,Tail,New),ucs(A,New,R).
ucs(A,[_|Tail],R):-ucs(A,Tail,R).
prolong(w(C,[X|T]),w(C1,[Y,X|T])):-e(X,Y,E),not(member(Y,T)),C1=C+E.
place([],L,L).
place([X|T],L,R):-placeone(X,L,L1),place(T,L1,R).
placeone(w(C,P),[w(C1,P1)|Tail],[w(C,P),w(C1,P1)|Tail]):-C<=C1,!.
placeone(X,[H|Tail],[H|NewTail]):-placeone(X,Tail,NewTail).
placeone(X,[],[X]).
%short_path
%ee toze ne legko obyasnit, chitaite v knige pro poisk v glubinu na str 161
short_path(A,B,P):-weight(A,[[B]],P).
append([],B,B). %esli pervii spisok pustoi, to rezultat - vtoroi spisok
append([H|Tail],B,[H|NewTail]):-append(Tail,B,NewTail). %esli ne pustoi, to rekursivno soedinyaem
%hvost pervogo spiska so vtorim spiskom i poluchaem tem samim hvost itogovogo spiska
n([H|Tail],[B,H|Tail]):-e(H,B,_),not(member(B,Tail)).
weight(A,[[A|T]|_],[A|T]):-!.
weight(A,[H|Tail],Ans):-findall(B,n(H,B),Temp),!,append(Tail,Temp,New),weight(A,New,Ans).
weight(A,[_|Tail],Ans):-weight(A,Tail,Ans).
%cyclic
%vipolnyaetsya proverka, chtobi kolichestvo vershin v grafe ne ravnyalos kolichestvu dug + 1
%lenght - vspomogatelnii predicat, schitaet dlinu spiska
lenght([],0). %dlina pustogo spiska ravna 0
lenght([_|Tail],L):-lenght(Tail,L1),L=L1+1.%dlina ne pustogo spiska ravna dline hvosta + 1
%q - vspomogatelnii predivat, kototii schitaet skolko v dannom spiske razlichnih vershin
q([],0).%esli spisok pust, to rezultat 0
q([H|Tail],N):-member(H,Tail),!,q(Tail,N). %esli pervii element vstrechaetsya v hvoste,
%to ego ne schitaem v otvete, a prosto rekursivno schitaem otvet ot hvosta
q([_|Tail],N):-q(Tail,N1),N=N1+1.%esli ze pervii element ne vstrechaetsya v hvoste
%(iz-za otsecheniya mi mozem syuda popast tolko v etom sluchae),to schetaem skolko v hvoste i pribavlyaem 1
cyclic:-findall(X,e(X,_,_),L),q(L,N),lenght(L,M),M<>2*(N-1).%nahodim spisok vseh reber,
%schitaem skolko v grafe vershin N, skolko reber M, i proveryaem vipolnimost kriteriya
%is_connected
is_connected:-not(not_connected).%graf svyazan, esli net ne svyazannoi pari vershin
%not_connected - vspomogatelnii predicat, proveryayushii est li v grafe nesvyazannaya para vershin
not_connected:-e(A,_,_),e(B,_,_),A<>B,not(path(A,B,_)).%istenen, esli est dve vershini, dlya kotorih ne vipolnim predicat path
goal
path(e,a,P),write(P),nl,fail.
%min_path(e,a,P),write(P),nl,fail.
%short_path(e,a,P),write(P),nl,fail.
%cyclic.
%is_connected.
|