Общие указания к решению типовой задачи
Формулировка задачи.
Выpазить чеpез K и S объект с комбинатоpной хаpактеpистикой:
Ia = a, (1)
пользуясь постулатами α, β, µ, ν, σ, τ, ξ исчисления λ-конвеpсии.
Решение
• Сфоpмулиpуем постулаты, задающие отношение конвеpтиpу-
емости “=” :
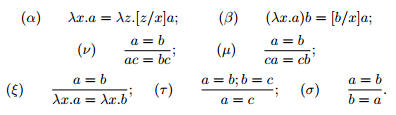
Определим комбинаторные характеристики объектов K и S:
v(Kxy) = vx, (K)
v(Sxyz) = v(xz(yz)), (S)
которые выражаются в λ-исчислении посредством K = λxy.x
и S = λxyz.xz(yz).
• Применяя схемы (K) и (S), убеждаемся в том, что:
a = Ka(Ka) (K)
= SKKa. (S)
Проверим, что действительно I = SKK. Пусть v = empty (пустой
объект).
• SKKa = Ka(Ka),
поскольку в схеме (S) можно положить
x = K, y = K, z = a.
Тогда ясно, что в силу постулата (α):
Sxyz = SKKa, xz(yz) = Ka(Ka), SKKa = Ka(Ka).
• Применяя аналогичным образом схему (K), заключаем, что
Ka(Ka) = a.
• По правилу транзитивности (τ), если SKKa = Ka(Ka) и
Ka(Ka) = a, то SKKa = a.
• Ответ. Объект I с заданной комбинаторной характеристикой
Ia = a имеет вид SKK, то есть I = SKK.
|
Главная
Каталог файлов
