Теоретические сведения. Вычисления с неподвижной точкой являются представлением цикличности в программах. Комбинаторная логика предоставляет специальный концепт-комбинатор Y , называемый комбинатором
неподвижной точки, который математически выражает цикл в вычислениях.
3.1 Абстракция
Для каждого терма M и переменной x терм [x]M, называемый абстракцией M по x, определяется индукцией по построению терма M:
(i) [x]x = I;
(ii) [x]M = KM, если x не принадлежит M;
(iii) [x]Ux = U, если x не принадлежит U;
(iv) [x](UV ) = S([x]U)([x]V ), если ни (ii), ни (iii) не подходят.
Пример 5. 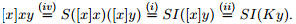
Теорема 1.
∀M, N, x : ([x]M)N = [N/x]M.
Доказательство см. в [77].
3.2 Мультиабстракция
Для переменных x1, . . . , xm (не обязательно различных) определим:
[x1, . . . , xm]M = [x1]([x2](. . .([xm]M). . .)).
Пример 1. 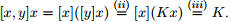
3.3 Локальная рекурсия
Важное применение комбинатора неподвижной точки дает использование в программах рекурсивных определений. Элементарно рассмотрим случай локальной рекурсии. Локальная рекурсия вида
E1 where x = . . . x . . .
преобразуется в
([x]E1)(Y ([x](. . . x . . .))),
где Y - комбинатор неподвижной точки, определяемый равенством:
Y f = f(Y f).
Для функции f выражение Y f - это неподвижная точка f . Взаимная
рекурсия в where-предложении вида
E1 where f x = . . . g . . .
g y = . . . f . . .
транслируется сначала в выражение:
E1 where f = [x](. . . g . . .)
g = [x](. . . f . . .),
из которого устранены переменные x и y. Затем пара взаимно ре-
курсивных определений преобразуется в одно общее рекурсивное
определение:
E1 where (f, g) = ([x](. . . g . . .),[y](. . . f . . .)),
которое может быть скомпилировано в выражение:
([f, g]E1)(Y ([f, g]([x](. . . g . . .),[y](. . . f . . .))))
с использованием уже известного правила. |