Теоретические сведения. Неформальное обсуждение понятия типа иллю-
стрирует довольно прозрачную идею. Всякая функция имеет область опре-
деления и область значения. Следовательно, не все аргументы предста-
вляют интерес, а только те из них, которые принадлежат выделенной
области определения. Это и означает, что аргументы как объекты типи-
зированы.
В аппликативных вычислительных системах в центре внимания не
области определения функций, а сами функции как общие законы соот-
ветствия. Фактически, исчисляются именно законы соответствия, или,
говоря иными словами, концепты функций, то есть в конечном счете объ-
екты. В этом случае для учета типов применяются более тонкие рассу-
ждения.
Действительно, комбинаторы задают функции, функции от функций,
функции от функций от функций, . . ., то есть возникают функции высших
порядков, или функционалы. Вопрос выяснения типа у объекта становится
нетривиальным, и типы приходится исчислять, пользуясь точными пра-
вилами. Соответствующие области определения становятся в сильной
степени взаимозависимы. В соответствующих логических конструкциях
можно прийти к противоречиям.
Перейдем на более точную основу в рассуждениях. Говорят, что тип
a приписан комбинатору X , или 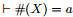 тогда и только тогда, когда тогда и только тогда, когда
данное утверждение вытекает из следующих аксиом и правила.
Схемы аксиом:
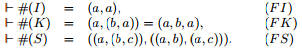
Правило:

Предлагается, пользуясь аксиомами и правилом (F), приписать типы основ-
ным комбинаторам:

В ходе решения этих задач предполагается уяснить, что такое ма-
тематические функции, как выполнять их композицию и как стро-
ить простейшие программы с помощью метода композиции. Каждый
комбинатор дает идеализацию программы в виде черного ящика. Это
значит, что внутренняя структура программы не уточняется, а важно
установить ее поведение, ориентируясь только на вход и выход. Ком-
бинации (композиции), составленные из комбинаторов, дают воз-
можность рассматривать произвольные программы как аппликатив-
ные формы. Аппликативная форма обладает простой структурой: ее
компоненты имеют левую и правую часть, поэтому представлением
формы служит бинарное дерево. Заметим, что отдельные ветви это-
го дерева можно вычислять независимо от других, что указывает на
потенциальный параллелизм вычислений.
Задача 6.1 Определить тип объекта B.
Указание. Построение S(KS)K представить в виде дерева:
Exp1 = (a1,(b1, a1))
Exp2 = a1
Exp3 = ((b1, a1),((a2, b2),(a2, c2)))
Exp4 = (b1, a1)
Exp5 = ((a2, b2),(a2, c2))
Exp6 = (a2, b2)
Exp7 = (a2, c2)
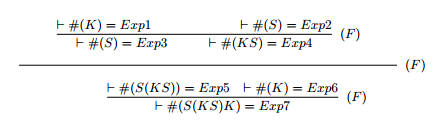
Решение.

Ответ. B имеет тип: # (B) = ((b, c),((a, b),(a, c))).
Аналогично определим типы, которые приписываются остальным
комбинаторам.
Задача 6.2 Тип # (SB).
Решение.
#(SB)--1. Построение дерева:
Exp1 = ((a1,(b1, c1)),((a1, b1),(a1, c1)))
Exp2 = (a1,(b1, c1))
Exp3 = ((a1, b1),(a1, c1))

Ответ.(SB) имеет тип (((b, c),(a, b)),((b, c),(a, c))).
Задача 6.3 Тип #(Z0).
Решение.
#(Z0)--1. Z0 = KI.
#(Z0)--2.

Ответ.Z0 = KI имеет тип (b,(a, a)).
Задача 6.4 Тип #(Z1).
Решение.
#(Z1)--1. Z1 = SB(KI).

#(Z1)--3. Exp1 = (((b1, c1),(a1, b1)),((b1, c1),(a1, c1)))
Exp2 = ((b1, c1),(a1, b1))
Exp3 = ((b1, c1),(a1, c1))
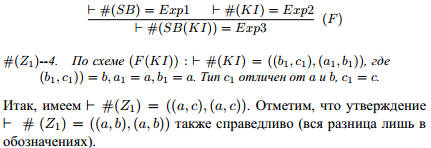
Ответ.Z1 = SB(KI) имеет тип ((a, b),(a, b)).
Задача 6.5 Тип #(Zn).
Решение.
• Определим сначала тип #(Z2).
#(Z2)--1. Z2 = SB(SB(KI)).

• Теперь определим тип #(Zn).

Задача 6.6 Тип #(W).
Решение.
#(W)--1. W = CSI.
#(W)--2. (F C) : ` #(C) = ((b,(a, c)),(a,(b, c))).
Это утверждение будет доказано далее.
#(W)--3. Exp1 = ((b1,(a1, c1)),(a1,(b1, c1)))
Exp2 = (b1,(a1, c1))
Exp3 = (a1,(b1, c1))
Exp4 = (a1)
Exp5 = (b1, c1)

Ответ. W = CSI имеет тип ((a,(a, b)),(a, b))




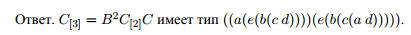
Задача 6.13 Тип #(Φ).
Решение.
#Φ--1. Φ = B2SB.
#Φ--2. Exp1 = ((b1 c1)((d1(a1 b1))(d1(a1 c1))))
Exp2 = (b1 c1)
Exp3 = ((d1(a1 b1))(d1(a1 c1))))
Exp4 = (d1(a1 b1))
Exp5 = (d1(a1 c1))
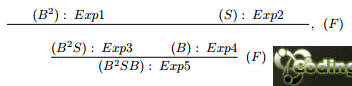
где (b1 c1) = ((a(b c))((a b)(a c))), (d1(a1 b1)) = ((b2 c2)((a2 b2)(a2 c2))).
Итак, d1 = (b2 c2) = (b2(b c)), a1 = (a2 b2) = (a b2), c1 =
((a b)(a c)). Пусть b2 = d; тогда (B2SB) : (d1(a1 c1)) =
((d(b c))((a d)((a b)(a c)))).
Ответ. Φ = B2SB имеет тип ((d(b c))((a d)((a b)(a c)))).
Задача 6.14 Тип #(Y ).
Решение.
#Y --1. Y = W S(BW B).

Следовательно, a = (b, b), (Y ) : (a, b) = ((b, b), b).
Ответ. Y = W S(BW B) имеет тип ((b, b), b).
Задача 6.15 Тип #(D).
Решение.
#D--1. D = C[2]I.
#D--2.
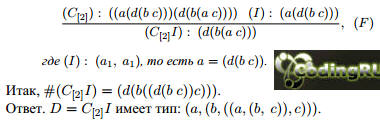
Задача 6.16 Тип #(C).
Решение.
#C--1. C = S(BBS)(KK)
#C--2. (S) : (a b c)((a b)(a c)), (B) : (b c)((a b)(a c)), (K) :
(a(b a)).
#C--3.

Итак, c3 = (a4 c4) = (b a c).
Ответ. C = S(BBS)(KK) имеет тип:((a,(b, c)),(b,(a, c))) |