Некоторым программам необходимы значения только половины записей в дву-
мерном массиве. Предположим, что у вас есть карта, на которой 10 городов обозна-
чены цифрами от 0 до 9. При помощи массива можно построить матрицу смежнос-
ти (adjacency matrix), хранящую информацию о наличии между парами городов
благоустроенных дорог. Элемент A[i, j] равен True, если между городами i и j есть
шоссе.
В таком случае значения в одной половине матрицы будут дублировать значе-
ния в другой, потому что A[i, j] = A[j, i]. Таким же образом в программу не будет
включен элемент A[i, i], так как нет смысла строить автостраду от города i в тот же
самый город. Значит, потребуются только элементы A[i, j] в левом нижнем углу,
для которых i > j. Можно с таким же успехом использовать элементы, находящие-
ся в правом верхнем углу. Поскольку все они образуют
треугольник, этот тип массивов называется треугольным
массивом (triangular array).
На рис. 4.1 изображен треугольный массив. Элемен-
ты со значимыми данными обозначены как X, ячейки, со-
ответствующие дублирующимся элементам, оставлены
пустыми. Незначащие диагональные записи A[i, i] обо-
значены тире.
Затраты памяти на хранение таких данных для не-
больших двумерных массивов не слишком существенны.
Если же на карте много городов, то напрасный расход па-
мяти может оказаться значительным. Для N городов будет N*(N- l)/2 дублиро-
ванных элементов и N элементов, подобных A[i, i], которые не являются значи-
мыми. Если карта содержит 1000 городов, то в массиве будет храниться больше
полумиллиона ненужных элементов.

Рис. 4.1. Треугольный массив
Вы можете избежать таких потерь памяти, создав одномерный массив В и упа-
ковав в него значимые элементы массива А.
Разместите записи в массиве В построчно, как показано на рис. 4.2. Обратите
внимание, что индексы массива перечисляются, начиная с 0. Это делает следую-
щие формулы немного проще.
Чтобы еще более упростить это представление треугольного массива, можно
написать функции для преобразования индексов массива А в индексы массива
В. Формула для преобразования A[i, j] в В[х] имеет следующий вид:
X := Round(i*(i-l)/2)+j; // Для i>j
Например, если i = 2 и j = 1, то получится х = 2* (2-1) /2 + 1 = 2. Это
означает, что А[2,1] отображается в позицию 2 в массиве В, как показано на рис. 4.2.
Помните, что массивы нумеруются, начиная с 0.
Эта формула справедлива только при i > j. Значения других записей массива А
не передаются в массив В, потому что они избыточны или незначимы.
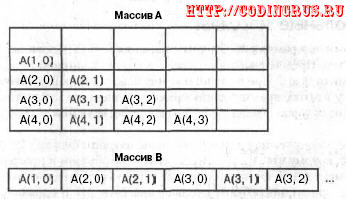
Рис. 4.2. Упаковка треугольного массива в одномерный массив
Если нужно получить значение A[i, j], где i < j, вы можете вычислить значение
A[j,i].
Подобные вычисления достаточно сложны. Здесь требуются операции вычи-
тания, сложения, умножения и деления. На выполнение программы будет уходить
намного больше времени, если придется часто прибегать к таким операциям. Это
пример компромисса между пространством и временем. Упаковка треугольного
массива в одномерный экономит память, хранение данных в двумерной матрице
занимает больший объем памяти, но экономит время |