Подобно , кривые Серпинского - это самоподобные кри-
вые, которые обычно определяются рекурсивно. На рис. 5.5 изображены кривые
Серпинского с глубиной 1, 2, и 3.
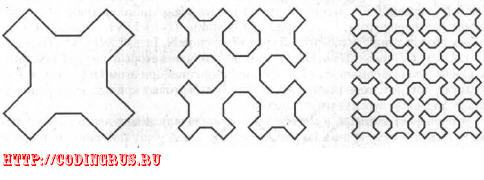
Рис. 5.5. Кривые Серпинского
Алгоритм построения Гильбертовых кривых использует одну процедуру для
рисования кривых. Кривые Серпинского проще строить с помощью четырех отдель-
ных процедур, работающих совместно, - SierpA, SierpB, SierpC. и SierpD. Эти
процедуры косвенно рекурсивные - каждая из них вызывает другие, которые после
этого вызывают первоначальную процедуру. Они выводят верхнюю, левую, ниж-
нюю и правую части кривой Серпинского соответственно.
На рис. 5.6 показано, как эти процедуры образуют кривую глубины 1. Отрез-
ки, составляющие кривую, изображены со стрелками, которые указывают направ-
ление их рисования. Сегменты, используемые для соединения частей, представ-
лены пунктирными линиями.
Каждая из четырех основных кривых составлена из линий диагонального сег-
мента, вертикального или горизонтального и еще одного диагонального сегмента.
При глубине рекурсии больше 1 необходимо разложить каждую кривую на мень-
шие части. Это можно сделать, разбивая каждую из двух линий диагональных сег-
ментов на две подкривые.
Например, чтобы разбить кривую типа А, первый диагональный отрезок де-
лится на кривую типа А, за которой следует кривая типа В. Затем без изменения
выведите линию горизонтального сегмента так же, как и в исходной кривой типа
А. И наконец, второй диагональный отрезок разбивается на кривую типа D, за ко-
торой следует кривая типа А. На рис. 5.7 изображен процесс построения кривой
2-го порядка, сформированной из кривых 1-го порядка. Подкривые показаны
жирными линиями.
На рис. 5.8 показано, как из четырех кривых 1-го порядка формируется пол-
ная кривая Серпинского 2-го порядка. Каждая из подкривых обведена пунктир-
ными линиями.

Рис. 5.6. Части кривой Серпинского Рис. 5.7. Составление кривой типа А из меньших частей
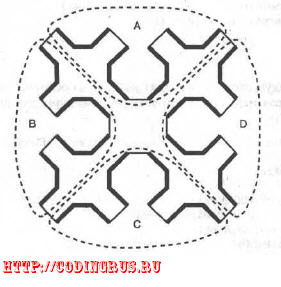
Рис. 5.8. Кривая Серпинского, образованная из меньших кривых
С помощью стрелок типа —» и <—, отображающих типы линий, которые соединя-
ют части кривых между собой (тонкие линии на рис. 5.8), можно перечислить рекур-
сивные зависимости между четырьмя типами кривых, как показано на рис. 5.9.
Все процедуры для построения подкривых Серпинс-
кого очень похожи друг на друга, поэтому здесь приведе-
на только одна из них. Зависимости, показанные на рис.
5.9, показывают, какие операции нужно выполнить, что-
бы нарисовать кривые различных типов. Соотношения
для кривой типа А реализованы в следующем коде. Ос-
тальные зависимости можно использовать, чтобы изме-
нить код для вывода других типов кривых.

рис5.9 рекурсивные зависимости между кривыми Серпинского
procedure TSierplForm.SierpA(depth, dist:integer);
begin
with DrawArea.Canvas do
begin
if (depth = 1) then
begin
LineTo(PenPos.X-dist,PenPos.Y+dist);
LineTo(PenPos.X-dist,PenPos.Y+0);
LineTo(PenPos.X-dist,PenPos.Y-dist);
end else begin
SierpA(depth-l,dist);
LineTo(PenPos.X-dist,PenPos.Y+dist);
SierpB(depth-l,dist);
LineTo(PenPos.X-dist,PenPos.Y+0);
SierpD(depth-l,dist);
LineTo(PenPos.X-dist,PenPos.Y-dist);
SierpA(depth-l,dist);
end;
end;
end;
Кроме процедур, которые выводят каждую из основных кривых, требуется
процедура, которая использует эти четыре процедуры для построения полной
кривой Серпинского.
procedure TSierplForm.DrawSierp(depth, dist : Integer);
begin
with DrawArea.Canvas do
begin
SierpB(depth,dist);
LineTo(PenPos.X+dist,PenPos.Y+dist);
SierpC(depth,dist);
LineTo(PenPos.X+dist,PenPos.Y-dist);
SierpD(depth,dist);
LineTo(PenPos.X-dist,PenPos.Y-dist);
SierpA(depth,dist);
LineTo(PenPos.X-dist,PenPos.Y+dist);
end;
end;
|