При симметричном обходе упорядоченных деревьев узлы посещаются в по-
рядке сортировки, что очень полезно. Например, при симметричном обходе дере-
ва, изображенного на рис. 6.20, узлы посещаются в порядке 2, 4, 5, 6, 7, 8, 9.
Это свойство симметричного обхода упорядоченных деревьев приводит к про-
стому алгоритму сортировки:
1. В сортированное дерево добавляется элемент.
2. Элементы выводятся с помощью симметричного обхода.
Этот алгоритм работает достаточно хорошо. Но если вы добавляете элементы
в каком-либо определенном порядке, то дерево может стать длинным и тонким.
На рис. 6.21 изображено дерево, которое может получиться при добавлении элемен-
тов в порядке 1,6,5,2,3,4. Другие последовательности тоже могут привести к появ-
лению тонких и длинных деревьев.

Рис. 6.20. Симметричный обход сортированного дерева: 2, 4, 5, 6, 7,8,9
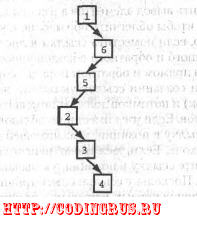
Рис. 6.21. Дерево, образованное при добавлении элементов в порядке 1, 6, 5, 2, 3, 4
Чем длиннее становится дерево, тем больше понадобится времени, чтобы до-
бавить элемент в его конец. В худшем случае после того, как вы добавите N эле-
ментов, дерево будет иметь высоту O(N). Общее время, необходимое для разме-
щения всех элементов в дереве, будет равно O(N^2).
Поскольку для обхода дерева требуется время O(N), полное время, необходи-
мое для сортировки чисел с помощью дерева, будет порядка O(N^2) + O(N) = O(N^2).
Если дерево достаточно короткое, его высота будет порядка O(log N). В таком
случае для добавления элемента требуется всего O(N) шагов.» На вставку всех N
элементов необходимо O(N * log N) шагов. И для сортировки элементов с помо-
щью дерева потребуется O(N * log N) + O(N) = O(N * log N) шагов.
Это гораздо меньше, чем О(N^2). Например, для построения высокого, тонкого
дерева, содержащего 1000 элементов, потребовалось бы около миллиона шагов.
Формирование короткого дерева высоты O(log N) займет всего порядка 10 000
шагов.
Если элементы дерева изначально расположены в случайном порядке, форма
дерева будет чем-то средним между этими двумя крайними случаями. Поскольку
его высота может оказаться несколько больше, чем log N, оно не будет слишком
высоким и тонким, поэтому алгоритм сортировки выполнится достаточно быстро. |