При нисходящей начинается с конца, с момента N и номер шага постепенно уменьшается на 1.
'факт' (N,F):-N1 is N-1, 'факт' (N1,F1), F is F1*N.
В качестве терминальной ситуации выбираются начальные условия. Условия окончания используются как значения аргументов целевого утверждения - запроса: ? - 'факт' (3,F).
Все это хорошо прослеживается в примерах 1, 2, где использована техника нисходящей рекурсии. Термин "нисходящая" происходит от термина "нисходящее проектирование" и обозначает то же самое, т.е. разбиение основной задачи на более простые подзадачи. Особенностью разбиения в рекурсивном определении является то, что подзадачи являются подобными (т.е. копиями) исходной задачи, а более простыми они оказываются за счет других исходных данных.
Рассмотрим процесс нисходящей рекурсии для примера 1 (F=N!). Опишем его с помощью И-ИЛИ-дерева, представленного на рис.1, для запроса ? - 'факт'(3,F).
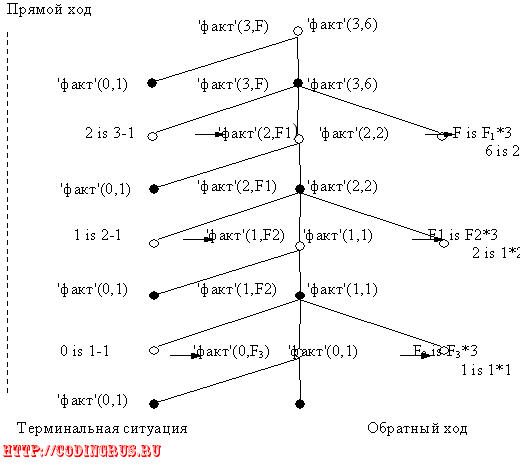
Рис 1.0
Из анализа схемы следует, что процесс выполнения рекурсивного определения можно разбить на три части:
• прямой ход - с момента ввода целевого утверждения до момента достижения терминальной ситуации;
• терминальная ситуация, соответствующая одному из граничных условий;
• обратный ход - с момента наступления терминальной ситуации до момента достижения вершины доказательства.
При нисходящей рекурсии прямой ход характеризуется тем, что выполняемая цель при согласовании с БЗ порождает и вызывает к выполнению новые, точно такие же цели, но с другими аргументами.
При этом не вычисляются никакие требуемые в задаче данные. В момент достижения терминальной ситуации результат решения задачи отсутствует. Он начинает строиться постепенно только при выполнении обратного хода (F is F1*N), в процессе которого осуществляется передача значений аргументов доказанной цели в тело вызвавшего ее правила.
Окончательный результат оказывается построенным только при достижении вершины. В этот момент его значение приобретает один из аргументов целевого утверждения-запроса, что позволяет использовать результат в дальнейшей части программы.
К достоинствам нисходящей рекурсии следует отнести простоту перехода от рекуррентных соотношений к программе и минимальное число аргументов в определяемом предикате. Однако нисходящая рекурсия требует большого объема памяти для хранения всех копий вызываемого рекурсивно предиката и является неэффективной по времени.
/* Нисходящая рекурсия */
'meaning'(N):-
'pr'(1,S,N),
write(S).
'pr'(K,P,K):-
P is (1/K).
'pr'(K,P,N):-
K1 is K+2,
'pr'(K1,P1,N),
P is 1/(K+P1).
|