При восходящей рекурсии моделирование процесса начинается сначала, с момента k=0. Номер шага постоянно возрастает: k=k+1. В качестве терминальной ситуации выбирается момент достижения условий окончания процесса k=N, начальные условия задаются в качестве значений аргументов целевого утверждения-запроса. В восходящей рекурсии параметры, характеризующие состояние процесса, вычисляются на каждой стадии рекурсии в процессе выполнения прямого хода. Ниже приведено определение процесса вычисления факториала F=3!, написанное с использованием техники восходящей рекурсии.
/* неправильное определение восходящей рекурсии */
'факт1'(3,P):- write(P), nl. /* терминальная ситуация */
/* описывает условия */
'факт1'(K,P):-K1 is K+1, P1 is P*K1,
/* P1 – текущее состояние процесса*/
'факт1'(K1,P1).
?-'факт1'(0,1). /* начальные состояние процесса */
В этом определении K и K1=K+1 - номера соответственно текущего и следующего шагов; P - промежуточное значение факториала, вычисленное к моменту K; следующее значение P1 определяется как P1=P*K1.
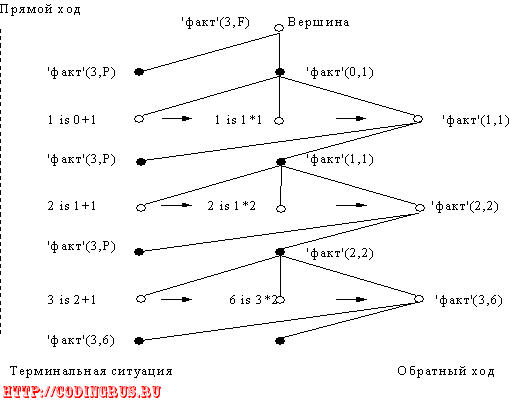
Рис.2
Как видим, огромным недостатком определения 'факт1' является зависимость описания терминальной ситуации от значений исходных данных. Например, для F=4! первое утверждение должно иметь вид 'факт1'(4,P). Проанализируем вычисление восходящей рекурсии с помощью И-ИЛИ-дерева, представленного на рис.2.
Из анализа схемы следует, что в процессе выполнения прямого хода результат строится постепенно (P хранит промежуточные значения) и окончательное значение приобретается в момент достижения терминальной ситуации. При обратном ходе результат теряется, так как восстанавливаются конкретизированные значения аргументов цели 'факт1'. Таким образом, в вершине доказательства результат отсутствует. Чтобы его не потерять, необходимо в момент достижения терминальной ситуации передать его значение переменной-результату, которую дополнительно необходимо включить в список аргументов. Избавиться от конкретики терминальной ситуации также можно введением еще одной переменной N в список аргументов, представляющей собой номер последнего шага процесса. С ее значением постоянно сравнивается номер текущего шага K, и при выполнении условия окончания процесса K=N достигается терминальная ситуация.
Таким образом, список аргументов предиката, проектируемого по схеме восходящей рекурсии, должен содержать две группы параметров: одна группа - это исходные данные и результат, вторая - промежуточные значения переменных процесса. Например:
'факт1'(N,F,K,P),
где N - исходное данное, F - результат, K - текущий номер, P - текущее состояние.
Чтобы сохранить число аргументов таким же, как и при нисходящей рекурсии, следует определить два разных предиката, один из которых (основной) обращается к предикату с дополнительно введенными аргументами и построенному по схеме восходящей рекурсии. Например:
/* правильное определение восходящей рекурсии */
'факт'(N,F):- /* основной предикат */
'факт1'(N,F,0,1). /* рекурсивно описанный предикат */
'факт1'(N,F,N,F):-!. /* терминальная ситуация */
'факт1'(N,F,K,P):- K1 is K+1, /* восходящая рекурсия */
P1 is P*K1, 'факт1'(N,F,K1,P1).
?-'факт'(3,F). /* запрос */
Достоинством восходящей рекурсии (рекурсивный вызов в конце тела правила) является экономия памяти. Необходимо хранить только параметры рекурсивно определенных целей 'факт1', а не все тело правила. Следствием этого является также эффективность восходящей рекурсии по быстродействию. Рекомендуется во всех случаях, когда это возможно, переходить от нисходящей рекурсии к восходящей. Ниже приведен пример восходящей рекурсии для многошагового итерационного процесса на примере получения чисел фибоначчи.
/* восходящая рекурсия */
'фибоначчи' (N,F):- 'фибоначчи' (N,F,1,1,0). /* начальные услови я */
'фибоначчи' (N,F,N,F,_):-!. /* условия окончания */
/* терминальная ситуация */
'фибоначчи' (N,F,K,F1,F0):- K1 is K+1,
F2 is F0+F1, /* F(K)=F(K-2)+F(K-1) */
'фибоначчи' (N,F,K1,F2,F1).
?- 'фибоначчи' (10,Z). /* запрос */
Здесь N - порядковый номер элемента последовательности чисел фибоначчи; F - число фибоначчи. |