Теоретические сведения. Одна из наиболее трудных проблем при разра-
ботке пользовательского (языкового) интерфейса состоит в правильном
встраивании приложения в программную среду. Как известно, ее решению
способствует объектно-ориентированное программирование. На практи-
ке определяется специальный набор классов, экспортирующий методы для
прикладных программ.
В математике такой прием известен под названием погружения, ко-
гда в объемлющей теории, называемой метатеорией, строятся объекты,
совокупность которых составляет встроенную теорию. Метатеория вы-
ступает в роли оболочки, а объекты встроенной теории могут адапти-
роваться по мере необходимости, причем не происходит выхода за рамки
метатеории. Рассмотрим использование этого приема на примере. В ка-
честве метатеории используем бестиповую комбинаторную логику. Будем
считать ее оболочкой объектов. В качестве встроенной теории построим
систему объектов вместе с их характеристическими равенствами, кото-
рые реализуют интерфейс LISP, то есть образуют функционально пол-
ный универсум рассуждений о списках и атомах. Под списком объектов,
как обычно, понимаем конечную последовательность объектов, среди ко-
торых могут быть другие списки.
Язык LISP, или ЛИСП, является, по существу бестиповым языком.
Его основные конструкции совпадают с конструкциями бестипового λ-
исчисления. Хорошо известно, что эти конструкции выразимы средства-
ми комбинаторной логики. Целью настоящего исследования является уста-
новление комбинаторных характеристик некоторых функций языка про-
граммирования.
Воспользуемся η−ξ-исчислениемλ-конверсий. Приведем постулаты, зада-
ющие отношение конвертируемости “conv” (обозначаемое знаком “=”):
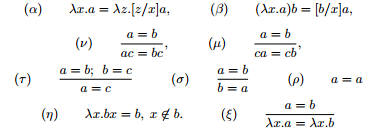
Формулировка задачи. Выразить с помощью комбинаторов следую-
щий набор функций LISP-системы:
{Append, N il, Null, List, Car, Cdr}. (LISP)
Уточненная формулировка задачи.
• Рассмотрим свойства этих функций языка LISP.
. Функция Append осуществляет конкатенацию двух спис-
ков. Эта функция обладает свойством ассоциативности:

где A, B, C - произвольные списки, знак “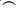 ” - инфикс- ” - инфикс-
ная форма записи функции Append.
. Пустой список обозначается как< >и эквивалентен обь-
екту Nil. Очевидно, что

. Функция Null распознает пустой список:
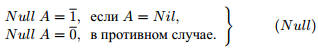
. ФункцияList строит из атома список длины 1:
Listx =< x >, (List)
где x - атом, < x1, x2, . . . , xn > - список длины n
. Функция Car выбирает первый элемент списка:
Car < x1, x2, . . . , xn >= x1. (Car)
. Функция Cdr убирает первый элемент из списка:
Cdr < x1, x2, . . . , xn >=< x2, . . . , xn > . (Cdr)
На основании этих свойств сформулируем следующие схемы
аксиом:

где a, b, c - произвольные обьекты.
• Докажем, что аксиомы (15.1)-(15.6) выводимы вη−ξ -исчислении
λ -конверсии.
Решение. Осуществим последовательный перевод содержательных
равенств (15.1)-(15.6) в термы и формулы комбинаторной логики.
LISP--1. Покажем, что функции Append соответствует обьект B с
комбинаторной характеристикой (B) : Babc = a(bc)(схема акси-
ом (15.1) ):
Ba(Bbc)x = a(Bbcx) (по схеме (B))
= a(b(cx)) (по схеме (B))
= Bab(cx) (по схеме (B))
= B(Bab)cx. (по схеме (B))
Учитывая правило транзитивности (τ), имеем:
Ba(Bbc)x = B(Bab)cx.
В η −ξ-исчислении доказуемо, что для переменной x:
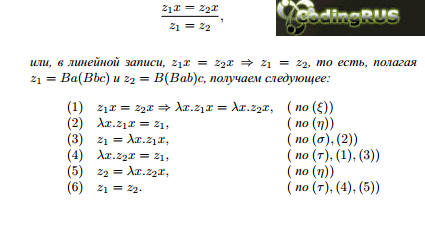
Итак, схема аксиом (15.1) доказана.
LISP--2. Докажем схему аксиом (15.2), принимая, что N il ↔ I выпол-
няется1, причем (I) : Ia = a.
BIax = I(ax) ( по (B))
= ax ( по (I))
= a(Ix) ( по (I))
= BaIx. ( по (B))
Поскольку BIax = BaIx, то BIa = BaI. Это заключение устана-
вливается приемом, аналогичным примененному в ходе обоснования
предыдущей аксиомы. Поскольку он будет применяться достаточ-
но часто, то специально сформулируем соответствующее правило:
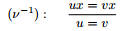
Это правило, как оказалось, работает в случае, когдаxявляется пе-
ременной. Если сопоставить его с одним из правил монотонности
(ν ), то можно заметить, что посылка и заключение в нем поменя-
лись местами


LISP--5. Аналогично, как и в предыдущем пункте, найдем объект, соот-
ветствующий функции Car:
a = Ka(bc) ( по схеме (K))
= Da(bc)K ( по схеме (D))
= B(Da)bcK ( по схеме (B))
= DcK(B(Da)b). ( по схеме (D)).
Очевидно, что DcK ↔ Car.
LISP--6. Тем же способом получим обьект соответствующий Cdr:
bz = I(bz) ( по схеме (I))
= KIa(bz) ( по схеме (K))
= Da(bz)(KI) ( по схеме (D))
= B(Da)bz(KI) ( по схеме (B))
= (λxy.xy(KI))(B(Da)b)z. ( по постулатам (β),(σ))

Решение поставленной задачи, безусловно, выполнено методом по-
гружения. Переформулируем его в терминах объектов.
Система равенств (15.1)-(15.6) в совокупности рассматривается
каксоотнесение, для которого индивидуализируется теория-оболочка.
Теория-оболочка представляется собой концепт, а результат индиви-
дуализации будет зависеть от выбора концепта. В качестве оболочки
выберем, например, η−ξ-исчисление λ-конверсий. Тогда каждый из
объектов-концептовAppend, N il, Null, List, Car, Cdr в результа-
те выполнения соотнесения даст соответствующий объект-индивид
B, I, D0(K(K0)), D, DcK, λxy.xy0. Объекты-индивиды образу-
ют теорию-индивид, которая представляет собой язык LISP (и явля-
ется оболочкой). У η − ξ-исчисления λ-конверсий проявляется одна
замечательная особенность: как объекты-концепты, так и объекты-
индивиды относительно соотнесения (15.1)-(15.6) остаются в рамках
одного и того же универсума. |