Логическая модель на основе на основе исчисления предикатов первого порядка.
Предикатом или логической функцией называется функция от любого числа элементов, принимающих значение “истина” или “ложь”.
Аргументы, принимающие значение из множества V, называются предметной областью.
Пусть F(x), G(x,y) – предикаты.
F и G – предикатные буквы.
x и y – предикатные переменные.
Одноместный предикат F(x) на предметном множестве M интерпретируется как x обладает свойством F.
N-местный предикат F(x1, x2, …,xn) интерпретируется как x1, x2, …,xN находятся в отношении F.
Существует инфиксная форма:
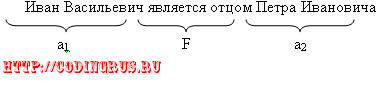
Префиксная: является отцом (Иван Васильевич, Петр Иванович)
1) Исчисление предикатов как формальная система.
- множество исходных элементов.
F – правило построения формул из элементов.
А – множество аксиом.
R – множество правил вывода.
1.1 B: — предметные переменные x1, y1,…
ниже И – переменные.
выше И – константы.
— предметные константы
(Иван Васильевич, РГРТА)
— предикатные символы
(F, является отцом)
— функционирующие символы plus (x, y, z)
— связи (┐, &, v, →, ???)
A → B – импликация
2)
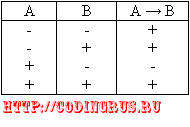
A → B = ┐A v B
Пример. Если пройдет дождь, то будет урожай. Из этого не следует, что если есть урожай, значит, был дождь.
Если урожая нет, значит, не было дождя.
(A → B) → (┐B → ┐A)
— ( ) “,”
— ├ - выводимость.
╞ - тождественная истина.
├ A – A выводится из аксиом.
C, В ├A – A выводится из C и D (или ???)
— квантор общности ? и квантор существования ?
Метод резолюций является методом математического доказательства теорем, основанных на получении логических следствий из множества S0, к которому добавлено отрицание гипотезы G .
Суть метода заключается в получении быстро уменьшающегося числа следствий. Каждое следствие (резольвента) получается из двух родительских дизъюнкта. Возможны различные стратегии выбора пары дизъюнктов для вывода очередного следствия. Для получения следствия естественно использовать принятые правила вывода Modus poneus.
├Р, ├Р→Q ├Р, ├ (┐РvQ)
Q Q
(A→B= ┐AvB) из этой формулы легко можно сделать вывод о возможных кандидатах на выбор очередной пары родительских дизъюнктов. Очевидно, что один из дизъюнктов должен содержать Р, другой – Р.
С1: Р
С2: ┐РvQ P и ┐P – контрарная пара
Q
Пример: S0={PvQ, ┐PvQ, Pv┐Q}
G=P&Q ?
(PvQ)&(┐PvQ)&(Pv┐Q)→P&Q
┐G=┐Pv┐Q, тогда
S={PvQ, ┐PvQ, Pv┐Q, ┐Pv┐Q}
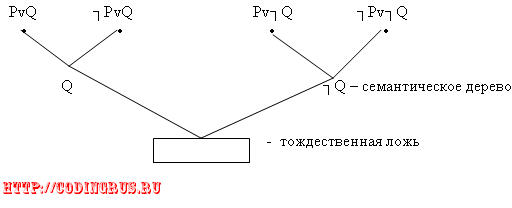
S0 – верно. Значит
G – ложь, G – истина.
Дж. Робинсон обобщил одно литеральное правило на случай произвольного дизъюнкта с произвольным числом литер.
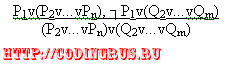
Пример: C1=PvQ
Bi=┐PvQ
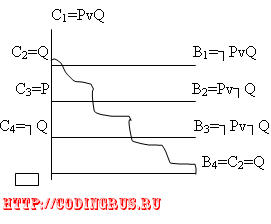
Для Хорновских дизъюнктов:

G=P→┐U ┐G=┐Pv┐U=P&U
|