Методические указания
1. При выборе способа представления графа для программирования предикатов группы IV следует учесть следующее. При простейшем, неявном способе задания графа легче программировать предикаты 16-18, однако он не применим для задания несвязных графов и работы с ними. Задание графа в виде терма - менее экономный способ, поскольку информация в нем частично дублируется, но он более универсален.
Кроме того, возможны и другие, еще более неэкономные и сложные способы представления (задания) графа, облегчающие в то же время его обработку; например, задание графа как списка пар вида
pair(<вершина>, <список вершин, смежных с ней>),
где pair - бинарный функтор. Для примера графа на рис. 2 таким списком будет
[pair (a, [b, c]), pair(b, [a, d]), pair(c, [a, d]), pair(d, [b, c, e]), pair(e, [d])].
При программировании некоторых предикатов может оказаться полезным перевод графа из одной формы представления в другую.
При любом способе задания графа кючевым моментом является то, что необходимо заранее решить, является ли обрабатываемый граф ориентированным или нет.
2. Несмотря на внешнюю похожесть определений предикатов min_path и short_path их эффективная реализация на Прологе требует применения разных алгоритмов поиска путей, т.е. перебора вершин в графе.
Нахождение минимального по стоимости пути предполагает полный просмотр графа и путей в нем. Такой просмотр целесообразно программировать на основе алгоритма поиска вглубь (depth_first_search), поскольку он по сути встроен в пролог-интерпретатор. При поиске вглубь всегда для продолжения просмотра из еще не рассмотренных вершин графа выбирается вершина, наиболее удаленная от начальной вершины (т.е. от которой был начат поиск) [Братко, с.330-335; Стерлинг, с.224-232].
Алгоритм поиска вглубь просто программируется и эффективно реализуется на Прологе, поскольку сам пролог-интерпретатор при доказательстве целей просматривает и обрабатывает альтернативы именно стратегией в глубину.
В отличие от min_path нахождение самого короткого пути (предикат short_path) в общем случае не требует полного просмотра графа; наиболее быстрое обнаружение такого пути гарантируется другим алгоритмом перебора вершин графа - алгоритмом поиска вширь (breadth_first_search). Для этого алгоритма характерно то, что всегда для продолжения поиска выбирается одна из вершин, наиболее близких к начальной.
Как и алгоритм поиска вглубь, поиск вширь является полным алгоритмом, т.е. при необходимости просматривает граф полностью, но порядок просмотра существенно иной.
Программирование на Прологе алгоритма поиска вширь существенно сложнее, так как для этого требуется сохранять и модифицировать в процессе перебора список всех путей, ведущих от начальной вершины к вершинам, от которых можно продолжать поиск [Братко, с. 336-344].
При программировании поиска вширь может оказаться полезным стандартный (встроенный) пролог-предикат второго порядка
findall (Var, Goal, Vlist),
где Var - переменная, Goal - предикат, имеющий в качестве одного из своих аргументов переменную Var, Vlist - выходная переменная - список возможных решений Goal. Сам findall детерминированный, его выполнение означает доказательство Goal в режиме бектрекинга: после каждого успешного окончания доказательства найденное значение Var добавляется в список Vlist и автоматически вырабатывается неуспех - до тех пор, пока не будут рассмотрены все варианты доказательства Goal. По окончании этого процесса предикат findall считается доказанным, а значением единственного выходного аргумента findall будет список из найденных значений переменной var.
Например, в результате доказательства
findall (X, append (X, _, [a, b, c]), Xlist)
Xlist получит значение ([a], [a, b], [a, b, c]).
3. Основой пролог-интерпретатора является встроенные механизмы унификации (сопоставления) и бектрекинга (возвратов). Для написания более эффективного варианта программы необходимо применять разностные структуры (списки, очереди и др.), позволяющие избегать ненужного копирования и просмотра структур (термов) в памяти за счет использования механизма сопоставления [Стерлинг, с.190-197].
Наиболее часто используются разностные списки, идея которых связана с тем, что каждый список можно представить как разность двух других списков, причем не одним способом. Например, для списка [1,2,3] возможны следующие варианты:
dl ([1,2,3,4,5], [4,5])
dl ([1,2,3| У], У)
dl ([1,2,3], [])
Здесь dl - бинарный функтор для представления разностного списка, т.е. разности двух списков: первый его аргумент - уменьшаемое (укорачиваемое), второй - вычитаемое.
Таким образом, разностный список - другое представление обычного списка, при котором вычитаемый список (второй аргумент функтора dl) фиксирует конец обычного списка, и он становится сразу доступен в процессе сопоставления, без просмотра обычного списка от начала до конца. Поэтому если два обычных списка соединяются в один список предикатом append за время, линейное от длины первого аргумента, то два неполных разностных списка могут быть соединены в разностный список за константное время. Причем реализуется это преобразование - разностный append - одним предложением
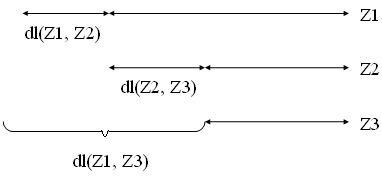
append_dl (dl (Z1, Z2), dl (Z2, Z3), dl (Z1, Z3) ).
Обоснованием этого предложения служит следующий схематический рисунок разностных списков:
|