Следующий пример демонстрирует возможности ООП-программирования при разработке новых программ на основе ранее созданных.  Свойства наследования и полиморфизма позволяют существенно экономить трудозатраты за счет использования ранее созданных объектов. Пусть ставится задача моделирования качения квадрата по некоторой, достаточно гладкой, криволинейной поверхности (рельефу)(рис. 10). Новый объект TScreen1, удовлетворяющий условиям задачи, может быть получен наследованием из объекта TScreen. Он содержит дополнительное поле Ground в виде целочисленного массива ординат рельефа и поле Sides0 для промежуточного хранения предыдущих координат сторон квадрата в процессе качения. Очевидно, что должны быть переопределены методы Init, DrawGround, ShiftOsXY и Go. Кроме того, понадобятся новые методы CalcABC и Dist для реализации подалгоритмов переопределяемых методов.

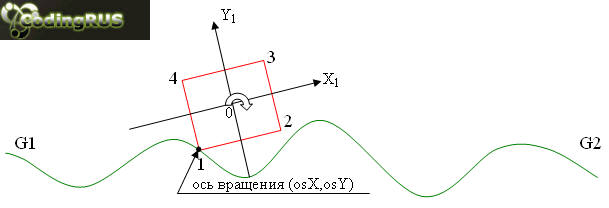
Рис. 10. Качение квадрата по криволинейной поверхности.

Далее приведен текст программы, полученный указанным способом.

{*********** Качение квадрата по заданному рельефу ************}

Program PrimerМ_OOP;

Uses  SqUnit, Crt, Graph;

Const sizeSq = 80;  colorSq = 12; colorG = 2;    deltaG = 400; 

Type  TScreen1 = Object( TScreen )

               Ground     :Array [ 0..n-1 ]  Of Integer;          { массив для рельефа}

               Sides0       :TSides;                          { буфер сохранения квадрата }

               Constructor Init   ( aa, colK, colG :Byte;  dG :Integer );

               Procedure   DrawGround;                  Virtual;

               Procedure   CalcABC ( Var S1,S2 :TLine; Var A,B,C :Real );

               Function    Dist( A, B, C, xx, yy :Real) :Real;    Virtual;

               Function    ShiftOsXY :Boolean;       Virtual;

               Procedure   Go;                                   Virtual;

               Destructor  Done;

           End;

Var  Screen1 :TScreen1;

(*****************  Методы TScreen1 *****************************)

{---------------------------------------------------------------}

Procedure   TScreen1 .DrawGround; {  рисование рельефа на экране }

Var i :Integer;

Begin

   SetColor(colorG);  ClearDevice;

   For i:=0 To 640 Do Begin MoveTo(i,Ground[i]); LineTo(i,GetMaxY); End;

End;

{---------------------------------------------------------------}

Constructor TScreen1 .Init ( aa,colK,colG :Byte;  dG :Integer );

Var   i, j, A1, T1, D1, A2, T2, D2:  Integer;

Begin

 Randomize;       { генерация амплитуды, частоты и фазы гармоник }

 A1:=Random(45)+5;    T1:=Random(40)+20;  D1:=Random(T1);

 A2:=Random(25)+5;    T2:=Random(40)+20;  D2:=Random(T2);

 For i:=0 To n-1 Do  { цикл заполнения ординат рельефа, dG-смещение }

  Ground[i] := dG + Round(A1 * Sin( i / T1 + D1)  +   A2 * Sin( i / T2 + D2 ));

 Gdisp := MaxInt;

 For i := 0 To aa Do  { поиск места начальной установки квадрата }

      If Ground[i] < Gdisp Then Begin Gdisp := Ground[i]; j:=i; End;

 Inherited Init ( aa, colK, colG, Gdisp-1 );       { инициализация квадрата }

 OsX:=j;                            { уст-ка координаты х оси вращения }

 DrawGround;                   { нарисовать рельеф }

End;

{---------------------------------------------------------------}

Function TScreen1 .Dist( A,B,C, xx,yy :Real) :Real;

{ ф-ция расстояния между прямой Ax+By+C=0 и точкой(xx,yy) }

Begin Dist := Abs((A*xx+B*yy+C) / Sqrt(A*A+B*B)); End;

{-------------------------------------------------------------------------}

Procedure  TScreen1 .CalcABC( Var S1,S2 :TLine; Var A,B,C :Real );

{ вычисление параметров A,B,C уравнения прямой, проходящей через центр } { квадрата параллельно двум его противоположным сторонам }

Var    xn,yn,xk,yk   :Real;

Begin  xn := (S1.pn.x+S2.pk.x)/2;  yn := (S1.pn.y+S2.pk.y)/2;

           xk := (S1.pk.x+S2.pn.x)/2;   yk := (S1.pk.y+S2.pn.y)/2;

            A := yk - yn;       B := xn - xk;     C := xk * yn - xn * yk;

End;

{-------------------------------------------------------------------------}

Function  TScreen1 .ShiftOsXY :Boolean;

{ Если в процессе качения какая-либо точка квадрата переходит границу }   { рельефа, то функция смещает ось вращения и возвращает True }

Var Ax, Bx, Cx, Ay, By, Cy, xx, yy :Real;     i :Integer;

Begin

  ShiftOsXY := False;

{ вычисление пар-ров прямых – осей локальной системы координат x10y1 }

  CalcABC( Sides[1], Sides[3],  Ax, Bx, Cx );

  CalcABC( Sides[0], Sides[2],  Ay, By, Cy );

  For i := OsX + 1  To  OsX + 3*as Div 2  Do  { перебор точек рельефа }

    Begin

     yy := Dist( Ay, By, Cy, i, Ground[i] ); { координаты i-ой точки рельефа }

     xx := Dist( Ax, Bx, Cx, i, Ground[i] );  {  в лок-ой системе   x10y1  }

     If ( xx <= as Div 2 + 1 ) And ( yy <= as Div 2 + 1 ) { если точка рельефа  }

      Then Begin                                                               {внутри квадрата , то}

                          Sides := Sides0;  { восст-ть предыд. положение  квадрата  }

                          OsX := i;     OsY := Ground[i];      {и сместить ось вращения }

                          ShiftOsXY := True;

                          Exit;

               End;

    End;

End;

{----------------------------------------------------------------------}

Procedure   TScreen1 .Go;     { моделирует движение квадрата }

Begin

 Repeat                                     { цикл возобновления сцены }

   Repeat                                   { цикл качения  по поверхности и анимации  }

     Repeat

          Sides0 := Sides;  { запоминание текущих коорд-т квадрата в буфере}

          Rotate ( OsX, OsY );    { вращение квадрата  вокруг текущей оси }

     Until Not ShiftOsXY;  { если была смена оси вращения, то пропустить }

     Show  ( Scolor );                  { рисует изображение квадрата }

     Delay ( ms );           { задержка  }

     Show  ( 0 );                           { стирает изображение квадрата }

     If KeyPressed Then Exit; { если клавиша нажата, то выход из процедуры}

   Until OsX > GetMaxX;       { если квадрат достиг правого края экрана, то }

   Init ( as, Scolor, Gcolor, deltaG );                                 { возобновление сцены }

 Until False;                     { повторение работы до нажатия любой клавиши }

End;

{----------------------------------------------------------------------}

Destructor  TScreen1 .Done;

Begin Inherited Done; End;

{----------------------------------------------------------------------}

{*********** Головная программа ****************************}

Begin

   With Screen1 Do Begin

       Init ( sizeSq, colorSq, colorG, deltaG );

       Go;

       Done;

    End;

End.

{***********************************************************}

Если каждая из полученных координат по абсолютной величине меньше половины длины стороны квадрата, то данная точка рельефа попадает во внутрь квадрата, поэтому данное положение квадрата не отображается на экране, а восстанавливаются предыдущие координаты квадрата (оператор Sides:=Sides0) и ось вращения перемещается в отмеченную ранее точку. Факт смены оси вращения отмечается в результате функции ShiftOsXY значением True. Метод Go обеспечивает перемещение квадрата и его отображение на экране, а алгоритм практически не отличается от прототипа в TScreen. Как видим, получение новой версии программы не потребовало существенных трудозатрат за счет использования преимуществ объектно-ориентированного программирования. Возможны дальнейшие модификации программы, например, перевести ее в режим двухстраничного отображения, что устранит мелькания изображения на экране.  Для более углубленного изучения ОО-программирования предлагается еще один более сложный пример.