Заметим, что ламбда-абстракции, как правило, не имеют имен. В от-
личие от них суперкомбинаторы имеют имена. Помимо этого супер-
комбинаторы могут ссылаться сами на себя. Это означает, что рекур-
сивные суперкомбинаторы реализуются непосредственно, без при-
влечения комбинатора неподвижной точкиY . Конечно, рекурсивные
определения можно преобразовать в нерекурсивные, воспользовав-
шись Y , но это потребует введения в употребление дополнительных
правил.
Пример 16.8 Для того, чтобы $F стал нерекурсивным, следует вве-
сти определения:
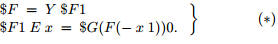
Дополнительное определение помечено символом “*”. Поскольку Y
необходимо редуцировать, то такое определение$F потребует боль-
ше редукций, чем рекурсивная версия.
Обозначение:
$S1 x y = B1
$S2 f = B2
. . .
E
эквивалентно выражению:
letrec
$S1 = [x].[y].B1
$S2 = [f].B2
. . . .
in
E.
Оно означает, что в E входят $S1, $S2, . . . , рекурсивные опреде-
ления которых приведены в letrec. Алгоритм ламбда-подъема рабо-
тает точно так же, как и ранее: выражения, встречающиеся в letrec,
понимаются так же, как и любые другие выражения. Тем не менее
возникает вопрос, какой лексический номер уровня следует припи-
сать переменным, связанным в letrec. Поскольку такие переменные
означиваются, когда непосредственно объемлющая абстракция при-
кладывается к аргументу, то их лексический номер совпадает с но-
мером данной абстракции. Если же объемлющей абстракции нет, то
лексический номер равен 0. Такой номер приписывается константам
и суперкомбинаторам. Внутри letrec, у которого нет абстракций, не
может быть никаких свободных переменных, кроме тех переменных,
которые уже определены в letrec. Такой letrec является комбинато-
ром. Для того, чтобы превратить его в суперкомбинатор, необходимо
выполнить ламбда-подъем, устраняющий все внутренние абстрак-
ции. Переменные, связанные в letrec уровня 0, не будут выноситься
как экстрапараметры, поскольку константы (напомним, что они име-
ют уровень 0) не выносятся.
Пример 16.9 Приведем программу, дающую бесконечный список еди-
ниц:
letrec x = cons 1 x
in x
В этой программе letrec находится на уровне 0, и абстракций нет,
поэтому x уже является суперкомбинатором:
$x = cons 1 x
$x
Пример 16.10 Рассмотрим рекурсивную функцию вычисления фак-
ториала:
letrec f ac = [n].IF(= n 0)1 (× n (f ac(− n 1)))
in f ac 4
В данном случае letrec имеет номер 0 и внутри [n].-абстракций нет.
Следовательно, f ac является суперкомбинатором:
$f ac n = IF(= n 0)1(×n(f ac(− n 1)))
$P rog = $f ac 4
$P rog
Упражнение 16.6 Скомпилировать программу:
let
inf = [v].(letrec vs = cons v vs in vs)
in
inf 4
Указание: let означает, что в выражении inf 4 функция inf имеет
определение, указанное в let. Функция inf v возвращает бесконеч-
ный список символов v. |