При решении задач чаще всего заранее неизвестно, сколько именно элементов исходного множества должно входить в искомое подмножество, то есть необходим перебор всех подмножеств. Однако, если требуется найти минимальное подмножество, то есть состоящее как можно из меньшего числа элементов (или максимальное подмножество), то эффективнее всего организовать перебор так, чтобы сначала проверялись все подмножества, состоящие из одного элемента, затем из двух, трех и т. д. элементов (для максимального подмножества — в обратном порядке). В этом случае, первое же подмножество, удовлетворяющее условию задачи и будет искомым и дальнейший перебор следует прекратить. Для реализации такого перебора можно воспользоваться, например, процедурой cnk, описанной в предыдущем разделе. Введем в нее еще один параметр: логическую переменную flag, которая будет обозначать, удовлетворяет текущее сочетание элементов условию задачи или нет. При получении очередного сочетания вместо его печати обратимся к процедуре его проверки check, которая и будет определять значение флага. Тогда начало процедуры gen следует переписать так:
procedure gen(m,L:integer);
var i:integer;
begin
if m=0 then
begin
check(p,k,flag);
if flag then exit
end
else ...
Далее процедура дословно совпадает с предыдущей версией. В основной же программе единственное обращение к данной процедуре следует заменить следующим фрагментом:
k:=0;
flag:=false;
repeat
k:=k+1;
cnk(n,1,flag)
until flag or (k=n);
if flag then print(k)
else writeln('no solution');
Очевидно также, что в основной программе запрос значения переменной k теперь не производится.
Существует также альтернативный подход к перебору всех подмножеств того или иного множества. Каждое подмножество можно охарактеризовать, указав относительно каждого элемента исходного множества, принадлежит оно данному подмножеству или нет. Сделать это можно, поставив в соответствие каждому элементу множества 0 или 1. То есть каждому подмножеству соответствует n-значное число в двоичной системе счисления (строго говоря, так как числа могут начинаться с произвольного количества нулей, которые значащими цифрами не считаются, то следует заметить, что в соответствие ставятся n- или менее -значные числа). Отсюда следует, что полный перебор всех подмножеств данного множества соответствует перебору всех чисел в двоичной системе счисления от
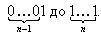
Теперь легко подсчитать и количество различных подмножеств данного множества. Оно равно 2^n – 1 (или 2^n, с учетом пустого множества). Таким образом, сопоставляя два способа перебора всех подмножеств данного множества, мы получили следующую формулу:
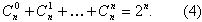
То есть, в рамках сделанной выше оценки на количество допустимых вариантов в переборе, мы можем рассмотреть все подмножества исходного множества только при n <= 20.
Прежде, чем перейти к рассмотрению программ, соответствующих второму способу перебора, укажем, когда применение этих программ целесообразно. Во-первых, данные программы легко использовать, когда необходимо в любом случае перебрать все подмножества данного множества (например, требуется найти все решения удовлетворяющие тому или иному условию). Во-вторых, когда с точки зрения условия задачи не имеет значения, сколько именно элементов должно входить в искомое подмножество. На примере такой задачи мы и напишем программу генерации всех подмножеств исходного множества в лексикографическом порядке. Задача взята из книги [5].
Условие. Дан целочисленный массив a[1..N] (N <= 20) и число M. Найти подмножество элементов массива a[i1], a[i2], ...a[ik] такое, что 1 <= i1 < i2 < i3 < ... < ik <= N и a[i1] + a[i2] + ... + a[ik] = M.
Решение. В качестве решения приведем процедуру генерации всех подмножеств, которые можно составить из элементов массива и функцию проверки конкретного подмножества на соответствие условию задачи.
function check(j:longint):boolean;
var k:integer; s:longint;
begin
s:=0;
for k:=1 to n do
if ((j shr (k-1))and 1)=1 {данное условие означает, что в
k-й справа позиции числа j, в 2-й системе, стоит 1}
then s:=s+a[k];
if s=m then
begin
for k:=1 to n do
if ((j shr (k-1))and 1)=1 then write(a[k]:4);
writeln
end
end;
procedure subsets(n:integer);
var q,j:longint;
begin
q:=1 shl n; {таким образом мы помещаем в q число 2^n}
for j:=1 to q-1 do {цикл по всем подмножествам}
if check(j) then exit
end;
Заметим, что если все элементы в массиве положительные, то, изменив порядок рассмотрения подмножеств, решение приведенной выше задачи можно сделать более эффективным. Так, если сумма элементов какого-либо подмножества уже больше, чем M, то рассматривать подмножества, включающие его в себя уже не имеет смысла. Пересчет же сумм можно оптимизировать, если каждое следующее сгенерированное подмножество будет отличаться от предыдущего не более, чем на один элемент (такой способ перечисления подмножеств показан в [2]). Приведенная же программа черезвычайно проста, но обладает одним недостатком: мы не можем ни в каком случае с ее помощью перебирать все подмножества множеств, состоящих из более, чем 30 элементов, что обусловлено максимальным числом битов, отводимых на представление целых чисел в Турбо Паскале (32 бита). Но, как уже было сказано выше, на самом деле, перебор всех подмножеств у множеств большей размерности вряд ли возможен за время, отведенное для решения той или иной задачи.
|