Этот алгоритм – усовершенствование прямых методов сортировки, являющийся сортировкой простыми вставками с убывающим шагом.
Эта сортировка основана на следующих положениях:
1. Сортировка простыми вставками очень эффективна для массивов, которые почти упорядочены.
2. Для малого числа элементов сортировка прямым методом с трудоемкостью порядка O(n2) часто более эффективна чем сортировка улучшенным методом из – за простоты реализации и отсутствия дополнительных действий, кроме сравнения и перестановок.
В методе Шелла сортировка простыми вставками применяется сначала к отдельным подмассивам(спискам) с малым числом элементов, что позволяет частично упорядочить весь массив. Затем сортировка с простыми вставками применяется к спискам с постепенно увеличивающимся количеством элементов.
Исходный массив:
а1…аn.
Введем h1 – шаг сортировки.
На 1ом этапе сортируется h1 списков с малым числом элементов. h1=4
1) а1,а5,a9 …
2) а2,а6,a10 …
3) а5,а7,а11…
4) а4,а8,а12…
На следующем этапе шаг сортировки уменьшается (выбирается h2 меньше h1) и процесс повторяется . Это выполняется для последовательности шагов h1…hk до того, как последний шаг k=1.
Пример. Пусть задан массив 25,57,48,37,12,92,86,33.
1) Сортируются 4 подмножества с помощью метода простых вставок (h1=4)
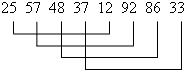
Получим:
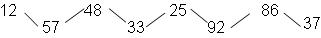
2) h2=2;
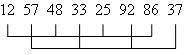
Получим:
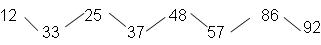
В общем случае значение шагов сортировки может быть произвольным( должно выполняться h1>h2>…>hn). Причем последний должен быть = 1.
При программировании значения этих шагов должны храниться в массиве. Чтобы не использовать массив, часто значения шагов задают следующим образом:
h1=[n/2]
h1=[h1/2]
Для удобства воспользуемся средствами basic
for i=1 to n
s=a(i)
for j=i-1 to 1 step -1
if s>=a(j) then goto 10
a(j+1)=a(j)
next j
10: a(j+1) = s
next i
Пусть k-номер сортируемого подсписка.
h-шаг сортировки.
Тогда
h=int(n/2)
While h>=1
For k=1 to h
for i=k+h to n step h
s=a(i)
for j=i-h to 1 step -h
if s>=a(j) then goto 10
a(j+h) = a(j)
next j
10: a(j+h)=s
next i
next k
h=int(h/2)
wend;
|