В комбинаторике такие подмножества называют сочетаниями из n элементов по k элементов и обозначают 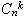 . Их количество выражается следующей формулой: . Их количество выражается следующей формулой:
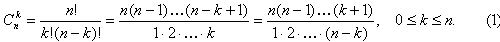
Однако при программировании гораздо удобнее использовать следующие рекуррентные соотношения:
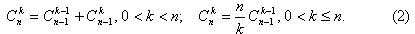
Объясняется это тем, что в формуле (1) числитель и знаменатель растут очень быстро, поэтому в силу особенностей компьютерной арифметики не всегда возможно точно вычислить значение Cnk, даже когда последнее не превосходит максимально представимое целое число.
При фиксированном значении n максимального значения число сочетаний достигает при k = n/2 (вернее, для четного n максимум один и он указан, а для нечетного — максимум достигается на двух соседних значениях k: [n/2] и [n/2]+1). Поэтому особенно полезной оказывается следующая оценка для четных n [4] (очевидно, что при нечетных n отличия будут минимальными), основанная на формуле Стирлинга:
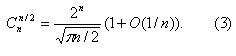
Если допустить, что за время, отведенное для решения задачи, мы можем перебрать около 106 вариантов, то из формулы (3) следует, что генерацию всех сочетаний из n элементов для любого фиксированного k можно проводить для n <= 24.
Обычно генерацию всех k-элементных подмножеств проводят в лексикографическом порядке, тем более что в данном случае это не приводит ни к усложнению алгоритма, ни к увеличению его вычислительной трудоемкости. Напомним, что порядок подмножеств называется лексикографическим, если для любых двух подмножеств справедливо, что раннее должно быть сгенерировано то из них, из индексов элементов которого можно составить меньшее k-значное число в n-ричной системе счисления (или в десятичной, для n < 10). Так, для n = 6 и k = 3 сочетание из третьего, первого и пятого элемента должно быть сгенерировано раньше, чем из второго, третьего и четвертого, так как 135 < 234.
Рассмотрим рекурсивный алгоритм решения данной задачи. Идея сведения данной задачи к задаче меньшей размерности следующая. Первым элементом подмножества может быть любой элемент, начиная с первого и заканчивая (n – k + 1)-м элементом. После того, как индекс первого элемента подмножества зафиксирован, осталось выбрать k – 1 элемент из элементов с индексами, большими, чем у первого. Далее поступаем аналогично. Когда выбран последний элемент, то мы достигли конечного уровня рекурсии и выбранное подмножество можно обработать (проанализировать или распечатать). В предлагаемой ниже программе массив a содержит значения элементов исходного множества и может быть заполнен произвольным образом. В массиве p будем формировать очередное сочетание из k элементов.
const nmax = 24;
type list = array[1..nmax] of integer; var k,i,j,n,q : integer; a,p : list; procedure print(k : integer);
var i:integer; begin for j:=1 to k do write(p[j]:4); writeln end;{print}
procedure cnk(n,k : integer); procedure gen(m,L : integer); var i:integer; begin if m=0 then print(k) else for i:=L to n-m+1 do begin
p[k-m+1]:=a[i];
gen(m-1,i+1)
end
end;{gen}
begin {cnk} gen(k,1) end;{cnk} begin {main} readln(n,k); for i:=1 to n do a[i]:=i;{заполнить массив можно и по-другому}
cnk(n,k)
end.
Заметим, что собственно генерация сочетаний производится в рекурсивной подпрограмме gen. Она имеет следующие параметры: m - сколько элементов из множества нам еще осталось выбрать и L - начиная с какого элемента исходного множества, следует выбирать эти m элементов. Обратите внимание, что именно вложенная структура описания процедур cnk и gen позволяет не передавать при рекурсивных вызовах значения n и k, а из основной программы обращаться к процедуре cnk с параметрами, соответствующими постановке задачи, не вдаваясь в подробности ее решения. Такой способ будем применять и в дальнейшем.
|