Число разбиений n-элементного множества на k блоков произвольного размера но таких, что каждый элемент множества оказывается “приписан” к одному из блоков, выражается числом Стирлинга второго рода S(n,k) [6,7]. Очевидно, что S(n,k) = 0 для k > n. Если согласиться, что существует только один способ разбиения пустого множества на нулевое число непустых частей, то S(0,0) = 1 (именно такая договоренность, как и в случае с факториалом, приводит в дальнейшем к универсальным формулам). Так как при разбиении непустого множества нужна по крайней мере одна часть, S(n,0) = 0 при n > 0. Отдельно интересно также рассмотреть случай k = 2. Если непустое множество разделили на две непустые части, то в первой части может оказаться любое подмножество исходного множества, за исключением подмножеств, включающих в себя последний элемент множества, а оставшиеся элементы автоматически попадают во вторую часть. Такие подмножества можно выбрать 2^(n-1) – 1 способами, что и соответствует S(n,2) при n > 0.
Для произвольного k можно рассуждать так. Последний элемент либо будет представлять из себя отдельный блок в разбиении и тогда оставшиеся элементы можно разбить уже на k – 1 частей S(n – 1,k – 1) способами, либо помещаем его в непустой блок. В последнем случае имеется kS(n – 1,k) возможных вариантов, поскольку последний элемент мы можем добавлять в каждый блок разбиения первых n - 1 элементов на k частей. Таким образом
S(n,k) = S(n – 1, k – 1) + kS(n – 1, k), n > 0. (5)
Полезными могут оказаться также формулы, связывающие числа Стирлинга с биномиальными коэффициентами, определяющими число сочетаний:
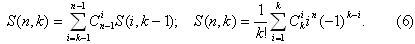
Если же значение k теперь не фиксировать и рассмотреть все разбиения n-элементного множества, то их количество выражается числом Белла
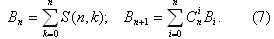
По формулам (7) можно подсчитать, что в рамках принятых выше допущений можно построить все разбиения множества, состоящего не более чем из 15 элементов (B15=1382958545).
Перейдем теперь к рассмотрению способа генерации всех разбиений исходного множества. Прежде всего следует договориться о том, как обозначать текущее разбиение. Так как в каждом из разбиений участвуют все элементы исходного множества, будем в массиве индексов p записывать в какой блок попадает каждый из элементов в текущем разбиении. Параметр i в рекурсивной процедуре part означает, что на текущем шаге мы именно i-ый элемент будет размещать в каждом из допустимых для него блоков, а j как раз и определяет максимальный номер допустимого блока. После того, как i-ый элемент помещен в один из блоков, рекурсивно решается такая же задача уже для следующего элемента (в данном случае фактически работает универсальная схема перебора с возвратом [8]).
procedure partition(n : integer; var p:list);
procedure part(i, j: integer);
var l: integer;
begin
if i > n then print(n, p) else
for l := 1 to j do
begin
p[i] := l;
if l = j then part(i+1, j+1)
else part(i+1, j)
end
end; {part}
begin {partition}
part(1,1)
end;
Как ни странно, в данном случае процедура print оказывается совсем не тривиальной, если требуется печатать (или анализировать) элементы каждого из блоков разбиения в отдельности. Поэтому приведем возможный вариант ее реализации (как и ранее, распределяли по блокам мы индексы, а печатаем или анализуруем сами элементы исходного массива a):
procedure print(n:integer; var p:list);
var i,j,imax:integer;
begin
imax:=1;{определяем количество блоков в разбиении}
for i:=2 to n do
if p[i]>imax then imax:=p[i];
for i:=1 to imax do {цикл по блокам}
begin
for j:=1 to n do
if p[j]=i then write(a[j]:4);
write(' |') {блок напечатан}
end;
writeln {разбиение напечатано}
end;
Вложенного цикла можно избежать, если требуется, например, подсчитать сумму элементов в каждом из блоков. Тогда, используя дополнительный массив, мы, просматривая элементы массива a последовательно, будем увеличивать значения суммы для блока, соответствующего рассматриваемому элементу (аналогично операции, осуществляемой в алгоритме сортировки подсчетом).
Если при этом рассматривать массив p как n-значное число n-ричной системе счисления, то можно ввести понятие лексикографического порядка для разбиений множества и ставить задачи определения номера разбиения и обратную ей. Как и ранее (см. [1-3]), они решаются методом динамического программирования и не используют непосредственную генерацию всех разбиений.
Для полноты рассмотрения данной темы самостоятельно измените процедуру partition так, чтобы она генерировала все разбиения, состоящие не более, чем из k блоков. После этого напишите процедуру разбиения множества уже на ровно k непустых частей.
|