Задание состоит из 5 задач, в которых требуется составить программы на Прологе. Первые две задачи требуют запрограммировать простые преди-каты. Следующие две - требуют написать простые программы. В последней задаче требуется составить более сложную программу на Прологе (как прави-ло, требуется определить несколько предикатов). При составлении программ (если не оговорено противное) можно использовать все встроенные предикаты Пролога. Тексты всех программ, если вы мыслите в духе логического про-граммирования, получаются небольшие.
SWI-Prolog не имеет стандартного help'а для Windows, для этого используется предикат help. Вызов help(<имя предиката>) выдает на экран информацию об этом предикате. Вызов help(7) выдает на экран список всех встроенных предикатов с комментариями. Текстовый файл руководства по SWI-Prolog - pl\library\manual. Отладку предикатов можно осуществлять с помощью предиката трассировки trace(<имя предиката>), трассировка преди-ката отключается - trace(<имя предиката>, -all).
Задание:
1. Напишите предикат p(+V, +X, -L) - истинный тогда и только тогда, когда список L получается из списка V после удаления всех вхождений X на всех уровнях, например, p([1, [2, 3, [1]], [3, 1]], 1, [[2, 3, []], [3]]) - истина.
2. Напишите обобщение предиката member, когда ищется элемент на всех уровнях в списке.
3. Встроенный предикат functor(+Term, ?Functor, ?Arity) определяет для за-данного составного терма Term его функтор Functor и местность Arity. Встроенный предикат arg(+N, +Term, ?Value) определяет для целого числа N и заданного составного терма Term его N-ый аргумент Value. Определите предикаты functor1 и arg1 - аналоги предикатов functor и arg через предикат univ (=..)
4. Напишите предикат range(?M, ?N, ?L), истинный тогда и только тогда, ко-гда L - список целых чисел, расположенных между M и N включительно (предикат должен допускать различное использование, когда не менее двух из трех аргументов конкретизованы). (Указание. Используйте предикаты var(+X) и nonvar(+X)).
5. Определим операторы:
:- op( 100, fy, ~).
:- op( 110, xfy, &).
:- op( 120, xfy, v).
Булева формула есть терм, определяемый следующим образом: кон-станты true и false - булевы формулы; если X и Y - булевы формулы, то и X v Y, X & Y, ~X - булевы формулы, здесь v и & - бинарные инфиксные операторы дизъюнкции и конъюнкции, а ~ - унарный оператор отрицания.
Напишите программу, задающую отношение negation_inward(+F1,-F2), которое выполнено, если логическая формула F2 получается из логической формулы F1 внесением всех операторов отрицания внутрь конъюнкций и дизъюнкций.
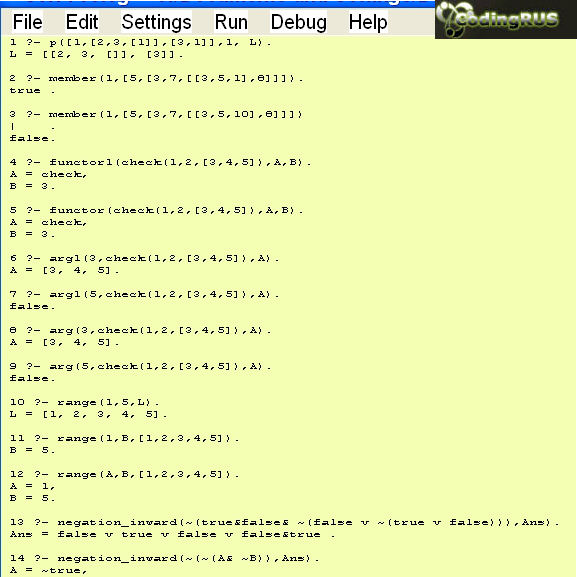
Исходный код программы:
p([X|Tail],X,NewTail):-!,p(Tail,X,NewTail).%esli golova iskomii simvol,
%to otvetom budet obrabotanni hvost
p([H|Tail],X,[NewH|NewTail]):-p(H,X,NewH),p(Tail,X,NewTail),!.%esli ze golova ne iskomii simvol,
%to ochishwem ee(srabotaet tolko esli ona - nepustoi spisok), ochishaem hvost i skladivaem
p(H,_,H).%esli golova ne iskomii simvol ili pustoi spisok, to nichego ne delaem
%?-p([1,[2,3,[1]],[3,1]],1, L),write(L).
member(H,H).%tut ponaytno
member(H,[A|B]):-member(H,A);member(H,B).%esli iskomii element vstrechaetsya v golove ili v hvoste,
%to on vstrechaetsya vo vsem spiske
member(H,[List]):-member(H,List).%eto esli spisok vida [[1,2,3,4,5]], to otbrasivaem odni skobki
%?-member(1,[5,[3,7,[[3,5,1],8]]]).
functor1(F,H,A):-F=..[H|Tail],length(Tail,A).
%element - vspomogatelnii predicat, vozvrashaet N-i element
element([H|_],1,H):-!.%pervii element - golova
element([_|Tail],N,E):-N1 is N-1, element(Tail,N1,E).%inache umenshaem index na 1 i ishem v hvoste
arg1(N,F,E):-F=..[_|Tail],element(Tail,N,E).
% ne znayu zachem v predicate range ispolzovat var i nonvar,i tak rabotaet
range(B,B,[B]):-!.
range(A,B,[A|Tail]):-A1 is A+1,range(A1,B,Tail).
%?-range(1,5,L).
%?-range(1,M,[1,2,3,4,5]).
%?-range(N,M,[1,2,3,4,5]).
:- op( 100, fy, ~).
:- op( 110, xfy, &).
:- op( 120, xfy, v).
%ne mogu garantirovat, chto imelos v vidu imeno tak vnosit,
%ya ispolzuyu zakoni Morgana i eshe ochevidnie fakti
negation_inward(~true,false):-!.
negation_inward(~false,true):-!.
negation_inward(~(A&B),NeA v NeB):-!,negation_inward(~A,NeA),negation_inward(~B,NeB).
negation_inward(~(A v B),NeA & NeB):-!,negation_inward(~A,NeA), negation_inward(~B,NeB).
negation_inward(~(~A),NewA):-negation_inward(A,NewA).
negation_inward(A&B,NewA & NewB):-!,negation_inward(A,NewA),negation_inward(B,NewB).
negation_inward(A v B, NewA v NewB):-!,negation_inward(A,NewA),negation_inward(B,NewB).
negation_inward(F,F).
%?- negation_inward(~(true&false& ~(false v ~(true v false))),Ans).
|