Можно получить большое количество различных комбинаторов, од-
нако оказывается, что эти комбинаторы не являются независимыми;
часть их можно определить через набор комбинаторов, называемых
базисными. Под комбинатором теперь можно понимать объект, со-
ставленный с помощью аппликаций из базисных комбинаторов.
Рассмотрим две базисные системы комбинаторов , W, B, K и
S, K:
xyz = xyz,
W xy = xyy,
Bxyz = x(yz),
Kxy = x;
Sxyz = xz(yz),
Kxy = x.
Для любого синтаксического объекта V , составленного из раз-
личных переменных x1, . . . , xn с помощью операции аппликации
можно найти комбинатор X, составленный из базисных, такой, что:
X x1, . . . , xn = V . Например, если V = xz(yz), то можно ука-
зать комбинатор X из базисной системы S, K, такой, что X xyz =
xz(yz). Как нетрудно видеть, им оказывается комбинатор S, то есть
X = S.
В общем случае поиск комбинатора X осуществляется посредством
следующих действий:
1) с помощью B из V удаляются скобки;
2) с помощью переменные переупорядочиваются;
3) с помощью W устраняются дублирования переменных;
4) с помощью K вводятся переменные, отсутствующие в V .
Пример 1. Построим в первой базисной системе комбинатор X со
свойством X abc = ac(bc):
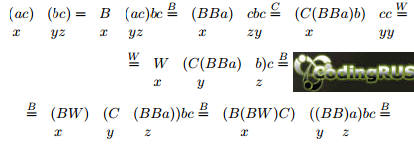
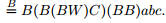
В этом примере под объектами, к которым можно применить заранее
известную схему, записаны переменные -- в том же порядке, что и
в соответствующей комбинаторной характеристике. Таким образом,
X = B(B(BW)C)(BB)
. |