Задача 20.1 Для выражения:
let x = plus in x (4,(x where x = 3)); ;
построить λ-выражение и выражение кода де Брейна и вычислить
последнее с помощью SECD-машины.
Решение.
DB--1. Известно, что в ходе выполнения λ -конверсии возника-
ют коллизии переменных. Например, “прямое” выполнение β-
редукции для (λxy.x)y могло бы дать λy.y:
(λxy.x)y = λy.y,
что совершенно недопустимо, поскольку:
Заметим, далее, что в замкнутом терме существенной важ-
ной информацией о переменной служит глубина ее связыва-
ния, то есть количество символов λ , стоящих между пере-
менной и связыванием λ (не считая последний оператор). То-
гда переменная оказывается замененной на число, которое,
однако, нельзя смешивать с обычным натуральным числом.
Для отличия числа, заменяющие переменные, от обычных на-
туральных чисел первые будем называть числами де Брейна.
Теперь, например, для
P = λy.(λxy.x)y
кодирование по де Брейну приобретает вид:
Скажем, правило (β), примененное к этому выражению, дает
λλ.1 , и нет необходимости в преобразовании λxy.x в λxv.x,
которое ликвидирует коллизию. Основной вопрос - это опи-
сание смысла выражений. Это зависит от ассоциаций значе-
ний и идентификаторов, то есть от среды. Таким образом,
означивание представляет собой функцию k M k, ассоцииру-
ющую значение со средой. Представим обычные семантиче-
ские равенства, где приложение функции к аргументу пред-
ставляется просто записью непосредственно вслед за симво-
лом функции символа аргумента:
k x k env = env(x),
k c k env = c,
k (MN) k env = k M k env(k N k env),
k λx.M k env d = k M k env[x ← d],
где:
env(x) - значение x в среде env;
c - константа, обозначающее значение,
также называемое c, что
соответствует обычной практике;
env[x ← d] - среда env, где x замещен на значение d.
Вообще, формализм де Брейна может быть рассмотрен по
аналогии с комбинаторной логикой с соответствующей ада-
птацией правил. Для осуществления перехода от обычных λ
-выражений к кодировке переменных числами де Брейна рас-
смотрим ряд правил и соглашений. Пусть среда env имеет
вид (. . .((), wn). . . , w0), где значение wi ассоциировано с чи-
слом i де Брейна. Такое предположения учитывает довольно
сильные ограничения. Среды, в которых происходит вычисле-
ние выражений, считаются связанными структурами, а не
массивами. Такой выбор тесно связан с выполнением требо-
вания эффективности. Прежде всего данный выбор ведет к
простому машинному описанию:
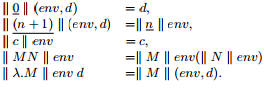
Интерес представляют не только значения сами по себе, а
значения с точки зрения обеспечиваемых ими вычислений. При
комбинаторном подходе подчеркивается, что значением, на-
пример, MN служит комбинация значений M и N.
Вводится три комбинатора:
S с арностью 2,
Λ c арностью 1, 0 c арностью 1
и бесконечно много комбинаторов n! в том смысле, что:
k n k = n!,
k c k env = c,
k MN k = S(k M k,k N k),
k λ.M k = Λ(k M k).
Отсюда легко устанавливается процедура перехода от се-
мантических равенств к чисто синтаксическим:
0!(x, y) = y,
(n+ 1)!(x, y) = n!x,
(0
x)y = x,
S(x, y)z = xz(yz),
Λ(x)yz = x(y, z)
Такие правила близки кSK-правилам: первые три указывают
на “забывающее” аргумент свойство (наподобие комбинато-
ра ); четвертое -- некаррированная форма правила S; пятое
-- в точности каррирование, то есть преобразование функции
от двух аргументов в функцию от первого аргумента, задаю-
щую функцию от второго аргумента.
Введем также комбинатор пары < ·,· >, где
k (M, N) k=,
и снабдим его выделителями (проекциями) F st и Snd. Вве-
дем также оператор композиции “◦” и новую команду ε. Рас-
смотрим S (·,·) и n! как сокращения для “ε◦ < ·,· >” и
“Snd ◦ F stn” соответственно, где F stn+1 = F st ◦ F stn.
Сведем теперь все комбинаторные равенства воедино:
(ass) (x ◦ y)z = x(yz),
(fst) F st(x, y) = x,
(snd) Snd(x, y) = y,
(dpair) < x, y > z = (xz, yz),
(ac) ε(Λ(x)y, z) = x(y, z),
(quote) (0
x)y = x,
где (dpair) устанавливает связь спаривания и образования со-
вокупности, а (acc)- композиции и аппликации. Можно заме-
тить, что S(x, y)z = ε(xz, yz). Тем самым придается од-
нородность рассмотрению операторов F st, Snd и ε . Кроме
того, справедливо равенство:
0
M = Λ(M ◦Snd),
откуда следует, что
(0x)yz = xz.
Пользуясь синтаксическими и семантическими равенствами,
получаем для M = (λx.x(4,(λx.x)3))+ :
M0 =k M k=k (λ.0(4,(λ.0)3))+ k
= S(k λ.0(4,(λ.0)3) k,k + k)
= S(Λ(k 0(4,(λ.0)3) k),k + k)
= S(Λ(S(0!,k (4,(λ.0)3) k)),k + k)
= S(Λ(S(0!, <0 4,S(Λ(0!),
0 3) >)),Λ(+◦Snd)).
DB--2. Теперь произведем вычисления по методу Лендина дляSECD-
машины, то есть следует означивать путем приложения 0 к
среде. В данном случае среда пуста, поскольку терм замкнут.
При означивании 0 применим стратегию самого левого и при
том самого внутреннего выражения. Для краткости обозна-
чим:
A = S(0!, <0 4, B >), B = S(Λ(0!),3).
Приведем полную последовательность редукций:
(Λ(A),Λ(+◦Snd))()
→ ε(Λ(A)(),Λ(+◦Snd)())
→ A env
(здесь: для сокращения env = ((),Λ(+◦Snd)()))
→ ε(0!env, <0 4, B > env)
→ ε(Λ(+◦Snd)(),(0
4 env, B env))
→ ε(Λ(+◦Snd)(),(4, B env))
→ ε(Λ(+◦Snd)(),(4, ε(Λ(0!)env,0 3 env)))
→ ε(Λ(+◦Snd)(),(4, ε(Λ(0!)env,3)))
→ ε(Λ(+◦Snd)(),(4,0!(env,3)))
→ ε(Λ(+◦Snd)(),(4,3))
→ (+◦Snd)((),(4,3))
→ +(Snd((),(4,3)))
→ +(4,3)
⇒ 7.
Видно,что результат совпадает с результатом, полученным
в ходе непосредственных вычислений выражения.
Контрольные вопросы.
1. Назовите альтернативные способы устранения коллизии пере-
менных в λ -выражениях.
2. Обоснуйте необходимость введения оператора композиции.
3. Покажите связь и различие между понятиями “пара” и “сово-
купность”.
Указание. Воспользуйтесь теоретико-множественными определени-
ями для этих понятий, положив f : D → E, g : D → F.
совокупность : h =< f, g >: D → E ×F;
пара : [f, g] = (f, g) : (D → E)×(D → F).
Упражнение. Постройте выражения де Брейна для приводимых да-
лее λ-выражений.
1. λy.yx.
Ответ: k λy.yx k= Λ(S(0!,1!)).
2. (λx.(λz.zx)y)((λt.t)z).
Указание. Обозначим исходное выражение черезQи перейдем
к выражению R = λzxy.Q. Тогда, рассмотрев дерево предста-
вления R, можем записать его в виде:
R0 = (λ.(λ.01)1)((λ.0)2),
и простой заменой “λ” на “Λ”, “◦” на "S", “n” на “n!” получить
код де Брейна для Q.
Ответ.
QDB(z,x,y) = S(Λ(S(Λ(S(0!,1!))1!)),S(Λ(0!),2!))
(порядок имен переменных в индексе Q соответствует поряд-
ку их связывания в промежуточном выражении R и позволяет
восстановить исходное определение с соответствующими сво-
бодными переменными). |