Теоретические сведения.Аббревиатура “КАМ” принята в качестве сокра-
щения для “Категориальная Абстрактная Машина”. Как можно видеть,
такое название само по себе несет значительную смысловую нагрузку.
• Сначала обоснуем введение самого термина “категориальная”. В
категориях пользуются композицией и тождеством (тождествен-
ное преобразование служит целям оптимизации), в декартовых ка-
тегориях дополнительно вводят произведение с использованием спа-
ривания < ·,· >, а также проекций F st и Snd. Декартово замкну-
тые категории (д.з.к.) дополнительно содержат каррирование Λ,
апплицирование ε и средства экспоненцирования, то есть средства
построения функциональных пространств.
Перечисленные в предыдущем разделе правила позволяют произво-
дить означивание категориальных термов видаM0
, построенных из
указанных комбинаторов путем аппликации (приложения) терма к
среде, которая построена из совокупности различных компонентов.
. Комбинаторы аппликации и построения совокупности не име-
ются в M0
. Аппликация возникает, когда записываем M(), то есть когда
категориальный терм прикладывается к (пустой) среде.
. Построение совокупности происходит всякий раз, когда ис-
пользуется правило (dpair).
Машинные инструкции такой КАМ строятся следующим образом:
статические операторы можно принять за базисные ма-
шинные инструкции.
Сперва отметим, что в применяемых при редукции M0
() правилах
все редексы имеют вид Mw, где w -- значение, то есть терм в нор-
мальной форме по отношению к применяемым правилам. Терм пре-
образован по де Брейну, то есть является кодом де Брейна.
. Рассматриваем терм как код, действующий на w, причем
образован из элементарных составляющих кода.
. Проекции F st и Snd с легкостью причисляются к набору ин-
струкций: F st действует на значение (w1, w2), образуя до-
ступ к первому порожденному элементу пары, если считать,
что значение представлено в виде бинарного дерева.
Для совокупностей рассматривается действие < M, N > на
w в соответствии с равенством:
< M, N > w = (Mw, Nw).
Действия M и N на w должны выполняться независимо, а затем
результаты объединяются в виде дерева, вершина которого явля-
ется совокупностью, а листья - полученными значениями w1 и w2 .
В последовательной машине сперва выполняется означивание, на-
пример . Получается w1. Перед началом обработки w его следует
сохранить в памяти, чтобы иметь возможность восстановить w
при означивании N, когда получается w2. Наконец w1 и w2 собира-
ются в совокупность, но в предположении, что запомнено значение
w1, а это выполняется именно в тот момент, когда восстанавли-
ваем w.
Исходя из рассмотренных выше соображений возникает структура
машины:
T − терм как структурированное значение, например граф;
C − код;
S − стек, или дамп (вспомогательная память).
Состоянием машины считается тройка < T, S, C >.
На основании предыдущего кодом для < M, N > считается следу-
ющая последовательность инструкций:
“<” , за которой следует последовательность инструкций,
соответствующая коду , за которой следует “,”, за которой
следует последовательность инструкций, соответствую-
щая коду N, за которой следует “>”.
• Отметим, что категориальная абстрактная машина (КАМ) совер-
шает только символьные преобразования, компиляция нигде не про-
водится. Достигается это с помощью следующих инструкций.
Представим действие инструкций “<”, “,”, “>”:
< : выталкивает терм на вершину стека,
, : меняет местами терм и вершину стека,
> : строит совокупность из вершины стека и терма, заме-
няет терм на эту совокупность и проталкивает стек.
Тот конкретный синтаксис, который используется для спаривания,
в точности соответствует образованию управляющих инструкций.
Эти инструкции должны замещать конструкцию спаривания. Тем
самым достигается комбинирование означиваний M и N в означи-
вание < M, N >.
• Применительно к структуре машины проекции F st и Snd можно
описать более точно:
F st : получает терм (s, t) и замещает его на s,
Snd : получает терм (s, t) и замещает его на t,
Код дляn!формируется изnи инструкции “F st”, за которой следу-
ет инструкция “Snd”. Для построения кода можно не предприни-
мать дополнительных усилий, если воспользоваться соглашением.
. Примем xy или x | y для обозначения композиции, которая в
обычной математической практике обозначается как y ◦ x.
При каррировании кодом Λ(M) служит Λ(C), где C - код .
Действие “Λ” описывается следующим образом:
Λ(C): замещает терм s на C : s, где C - код, инкапсу-
лированный в Λ .
. Обозначение C : s служит сокращением для “Λ(M)s”. С точ-
ки зрения правил перезаписи действие “Λ” пусто, поскольку
Λ(M)w является значением в силу того, что w - значение, сле-
довательно его нельзя перезаписать. Дадим перефразировку в
терминах действий:
действием Λ(M) на w является Λ(M)w .
Описание команды “Λ” приводит к построению замыкания,
как и в SECD-машине. Действительно, как подчеркивается
самим обозначением C : s, в качестве значения обрабатыва-
ется совокупность, построенная из кода, соответствующего
телу λ-выражения, и значения, которое предствляет собой
среду декларации функции, описанной посредством абстрак-
ции.
• Вернемся к операции аппликации из λ-исчисления. Ее запишем, как
ε◦ < M, N >. В виде правила запишем равенство:
(ε◦ < M, N >)w = ε(Mw, Nw) (= ε[Mw, Nw]).
Последняя запись, содержащая символы квадратных скобок, исполь-
зуется в обозначениях комбинаторной логики. Пусть (Mw, Nw)озна-
чено как (w1, w2), что является действием кода, ассоциированного
с < M, N >. Осталась инструкция “ε”, которая получает w1 =
Λ(P)w0
1 и производит ε(Λ(P)w0
1, w2) = P(w0
1, w2).
В терминах КАМ кодом, соответствующим ε◦ < M, N >, служит
код для < M, N > за которым идет “ε” со следующим эффектом:
ε получает терм (C : s, t), замещает его на (s, t), а остав-
шейся части кода устанавливает префикс .
Дополнительно нужны константы. Они требуются для базисных
констант, когда кодом для 0
C является 0
(C) со следующим действием:
0
C : замещает терм на инкапсулированную константу .
Для конструкций типа встроенной функций, например, для символа
сложения, используется кодирование, ранее уже рассмотренное:
кодом для 0
(op) служит Λ((op)), где (op) - это инструкция
Snd, за которой следует “op”.
Прежде чем приступить к построению полной таблицы инструк-
ций, вспомним соглашения об обозначениях для списков инструкций
Таблица 21.1: Цикл работы КАМ
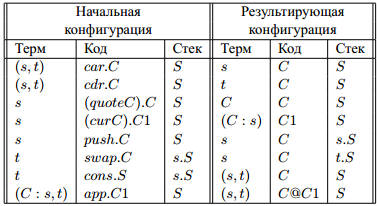
и элементов стека:
пустой список L обозначается через [];
обозначение [e1;. . .;en] принято для списка с n элемен-
тами e1, . . . , en;
a.L добавляет в начало L;
L1@L2 присоединяет L2 к L1.
Для удобства дадим инструкциям мнемонические наименования в
зависимости от их действия:
F st Snd < , > ε Λ 0
car cdr push swap cons app cur quote
Представим табл. 21.1, описывающую работу КАМ. В ее левой ча-
сти - начальные состояния (“старые”’ состояния), а в правой -
результирующие (“новые” состояния). Фактически, считаем КАМ
λ-исчислением с явными произведениями.
Фактически, в этой таблице описана система программирования
с небольшим числом исходных команд (инструкций). Заметим, что
среди них нет инструкции условного вычисления (условного перехо-
да). Эту инструкцию в дальнейшем приходится добавлять, пользу-
ясь некоторыми соглашениями, касающимися представления о ра-
боте категориальной абстрактной машины. Кроме того, при вычи-
слении рекурсивных определений приходится дополнительно обраба-
тывать (неявный) оператор неподвижной точки. Для этого снова
требуются дополнительные соглашения.
Задача 21.1 Для выражения:
let x = plus in x(4,(x where x = 3)); ;
построить его запись с помощью “категориального кода” и напи-
сать программу вычисления в терминах КАМ-инструкций.
Решение.
CAM--1. Воспользуемся математической символикой, которая под-
черкивает связь с правилами перезаписи. Пусть A, B обозна-
чают коды A и B соответственно, + служит сокращением
для plus, S(x, y) = S[x, y] = ε◦ < x, y >.
Результирующие вычисления представим в табл. 21.2. Отме-
тим, что вычисления начинаются с пустой средой, то есть в
позиции терма записан (). Исходный терм представлен в ви-
де кода де Брейна. В самом начале вычислений стек, или дамп
(“вспомогательная память”) также предполагается пустым
[].
Таким образом, КАМ позволила получить ожидаемый результат еще
одним способом, легко реализуемым на компьютере. Для этого сле-
дует иметь ввиду, что операция+не является собственно инструкци-
ей КАМ, но является встроенной в хост-систему программирования
функцией.
Контрольные вопросы.
1. Назовите три основных подхода к реализации языков функци-
онального программирования, лежащих в основе концепции
категориальной абстрактной машины.
2. Что представляют собой базисные машинные инструкции КАМ?
3. Опишите проекции Fst и Snd применительно к структуре ма-
шины.
Упражнение. Опишите таблицу машинных инструкций КАМ для вы-
числения выражения:
let x = 3 in (op(7, x) where op = sub).
Если вы открыли фирму в рязани и вам необходим сайт, тогда закажите его у профессионалов - http://www.abcwww.ru/services/sozdanie-sajtov.html. Здесь вам сделают быстро и качественно сайт.
Указание. Вначале получите соответствующее λ -выражение
(λx.(λop.op 7 x)sub)3,
на основе постулатов λ -исчисления преобразуйте его к виду
(λop.op(7,(λx.x)3))sub
и получите код де Брейна:
S(Λ(S(0!, <0 7,S(Λ(0!),
0 3) >)),Λ(sub ◦Snd)).
Теперь,переписав его в виде инструкций КАМ и выполнив необхо-
димые преобразования, можно получить ответ.
Ответ. 4.
Таблица 21.2: Вычисление на КАМ
 |