Существует много алгоритмов на графах, основанных на системном переборе их вершин таким образом, чтобы каждая вершина просматривалась один раз. Наиболее известным для этого методом является процедура, называемая поиском в глубину: Depth-First-Search (DFS).
Поиск в глубину на графе G=(V,E) осуществляется следующим образом:
Из некоторой вершины Vi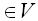 производится переход по ребру или дуге к любой вершине  , смежной к Vi. Если Vj уже просматривалась ранее, то выполняется возврат к вершине Vi и выбирается другая смежная вершина. Если же вершина Vj не просматривалась, то указанная процедура рекурсивно применяется к этой вершине. Процесс продолжается до окончания просмотра всех ребер или дуг, выходящих из вершины Vi. Далее происходит возврат к некоторой вершине , из которой ранее был произведен переход в вершину Vi и т.д. Конец процедуры поиска в глубину определяется условием, в соответствии с которым требуется выполнить возврат из вершины, с которой был начат просмотр вершин графа.
Рассмотрим возможный вариант реализации такой процедуры:
L(i) – список смежности i-ой вершины;
j принадлежит V(i) – выбор вершины j входящей в список смежности i – ой вершины;
mark[1..n] – определение состояния вершины:
mark(i)={true – вершина не просмотрена, false – вершина уже просмотрена}
for i:=1 to n do
mark[i]:=true;
for i:=1 to n do
if mark[i] then DFS(i);
{сама процедура поиска в глубину}
Procedure DFS(i:integer);
var j:integer;
begin
mark[i]:=false; write(i);
for j принадлежит L(i) do
if mark[j] then DFS(j);
end;
Время поиска в глубину пропорционально О(n+m) действий.
Ребра (дуги) исходного графа, приводящие в новые еще не просмотренные вершины, показываются сплошной линией и образуют ориентированное связанное дерево. Оно называется DFS-деревом. Его свойства:
- если исходный граф является не связным, то DFS-дерево представляется лесом. При этом для неориентированного дерева число компонент связанности леса равно количеству обращений к процедуре DFS (во внешнем цикле);
- для связанного ориентированного графа DFS-дерево может быть как связанным, так и не связанным в зависимости от его структуры и нумерации вершин.
- если в DFS-дереве есть путь из Vi в Vj, то Vi является предком для Vj и Vj является потомком для Vj. Ребро или дуга исходного графа, не вошедшая в DFS-дерево и направленная от потомка к предку – обратное ребро(дуга). Доказано, что если в графе есть цикл или контур, то при поиске в глубину обязательно встретиться обратное ребро или дуга. Указанные свойства DFS-деревьев используются в алгоритмах на графах, таких как выделение связанных компонент, поиск циклов, топологическая сортировка вершин и других.
|
Главная
Каталог файлов
