Теперь сосредоточим свое внимание на выработке технического навыка установления (и исследования свойств) нового концепта. В качестве таких концептов избираем различные комбинаторы, широко используемые в математической практике. Общая постановка задачи состоит в синтезе концепта-комбинатора по заранее заданной комбинаторной характеристике.
Задача 2.1 Вывод выражения для комбинатора B .
Формулировка задачи. Выpазить чеpез K и S объект с комбинатоp-
ной хаpактеpистикой:
Babc = a(bc), (B)
пользуясь постулатами α, β, µ, ν, σ, τ, ξ исчисления λ-конвеpсии.
Решение.
B--1. Сфоpмулиpуем постулаты, задающие отношение конвеpтиpуемости “=” :
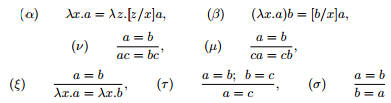
B--2. Определим комбинаторные характеристики объектов K и S:
x(Kyz) = xy, (K)
x(Syzw) = x(yw(zw)), (S)
которые выражаются в λ-исчислении посредством: K =
λxy.x и S = λxyz.xz(yz).
B--3. Применяя схемы (K) и (S), убеждаемся, что:
a(bc) = Kac(bc) (K)
= S(Ka)bc (S)
= KSa(Ka)bc (K)
= S(KS)Kabc. (S)
Проверим,что В = S(KS)K.
B--1. S(KS)Kabc = KSa(Ka)bc, поскольку в схеме (S) можно
положить x = (KS), y = K, z = a.
Тогда, в силу действия
постулата (α): Sxyz = S(KS)Ka, xz(yz) = (KS)a(Ka), т.е.
S(KS)Ka = (KS)a(Ka). Удалив несущественные скобки,
получим S(KS)Ka = KSa(Ka). Дважды применяя к полу-
ченному выражению постулат (ν), получим: S(KS)Kabc =
KSa(Ka)bc.
B--2. Аналогично, применяя схему (K), имеем KSa = S. Учиты-
вая постулат (ν), получим, что KSa(Ka)bc = S(Ka)bc.
B--3. Тем же способом, последовательно применяем схемы (S) и
(K), постулат (ν)и удаляя несущественные скобки, получаем:
S(Ka)bc = Kac(bc); (Kac)bc = a(bc).
B--4. Несколько раз применяя правило транзитивности (τ), полу-
чим S(KS)Kabc = a(bc). (Это выражение справедливо, по-
скольку если S(KS)Kabc = KSa(Ka)bc и KSa(Ka)bc = S(Ka)bc,
то S(KS)Kabc = S(Ka)bc и т.д.)
Ответ. Объект B с комбинаторной характеристикой
Babc = a(bc)
имеет вид S(KS)K, т.е. B = S(KS)K.
Задача 2.2 Вывод выражения для комбинатора C.
Формулировка задачи. Выpазить чеpезK, S и другие предварительно
определенные объекты объект с комбинатоpной хаpактеpистикой:
Cabc = acb, (C)
пользуясь постулатами α, β, µ, ν, σ, τ, ξ исчисления λ-конвеpсии.
Решение.
C--1. Сфоpмулиpуем постулаты, задающие отношение конвеpтиpу-
емости “=” (см. предыдущую задачу).
C--2. Напомним комбинаторные характеристики, возможно, ис-
пользуемых объектов:
(K) Kxy = x, (S) Sxyz = xz(yz), (I) Ix = x, (B) Bxyz = x(yz).
C--3. Применив эти схемы к (acb), получим:
acb = ac(Kbc) ( по схеме (K))
= Sa(Kb)c ( по схеме (S))
= B(Sa)Kbc ( по схеме (B))
= BBSaKbc ( по схеме (B))
= BBSa(KKa)bc ( по схеме (K))
= S(BBS)(KK)abc. ( по схеме (S))
Учитывая постулат транзитивности τ, имеем: S(BBS)(KK)abc =
acb
, т.е. C = S(BBS)(KK).
Ответ. Объект с комбинаторной характеристикойCabc = acb имеет
вид C = S(BBS)(KK).
Задача 2.3 Вывод выражения для комбинатора W.
Формулировка задачи. Выразить комбинатор W со следующей ха-
рактеристикой:
W ab = abb, (W)
Решение.
W--1. Выпишем характиристики используемых объектов:
(S) Sxyz = xz(yz), (I) Ix = x, (C) Cxyz = xzy.
W--2. Применим эти схемы к abb:
abb = ab(Ib) ( по(I))
= SaIb ( по(S))
= CSIab. ( по(C))
С учетом постулатов получаем: CSIab = abb, то есть
W = CSI.
W--3. Предложим еще два варианта вывода объекта W:
abb = ab(Kba) abb = ab(Kb(Kb))
= ab(CKab) = ab(SKKb) = Sa(SKK)b
= Sa(CKa)b = Sa(K(SKK)a)b
= SS(CK)ab = SS(K(SKK))ab.
Ответ. Объект W с характеристикой W ab = abb имеет вид: W =
CSI(= SS(CK) = SS(K(SKK))).
Задача 2.4 Вывод выражения для комбинатора Ψ.
Формулировка задачи. Выразить комбинаторΨсо следующей характеристикой:
Ψabcd = a(bc)(bd), (Ψ)
Решение.
Ψ--1. Сфоpмулиpуем постулаты, задающие отношение конвеpтиpуемости.
Ψ--2. Напомним комбинаторные характеристики используемых объектов:
(C) Cxyz = xzy, (W) W xy = xyy, (B) Bxyz = x(yz).
Ψ--3. Применив эти схемы к a(bc)(bd), получим:
a(bc)(bd) = B(a(bc))bd ( по схеме (B))
= BBa(bc)bd ( по схеме (B))
= B(BBa)bcbd ( по схеме (B))
= BB(BB)abcbd ( по схеме (B))
= C(BB(BB)ab)bcd ( по схеме (C))
= BC(BB(BB)a)bbcd ( по схеме (B))
= W(BC(BB(BB)a))bcd ( по схеме (W))
= BW(BC)(BB(BB)a)bcd ( по схеме (B))
= B(BW(BC))(BB(BB))abcd. ( по схеме (B))
Учитывая необходимые постулаты, получаем следующий результат: B(BW(BC))(BB(BB))abcd = a(bc)(bd)
, т.е. Ψ =
B(BW(BC))(BB(BB)).
Ответ. ОбъектΨс комбинаторной характеристикойΨabcd = a(bc)(bd)
имеет вид Ψ = B(BW(BC))(BB(BB)).
Задача 2.5 Вывод выражения для комбинатора B2.
Формулировка задачи. Выpазить чеpез K и S и другие предваритель-
но определенные объекты объект с комбинатоpной хаpактеpистикой:
B2abcd = a(bcd), (B2)
Решение.
B2--1. Сфоpмулиpуем постулаты, задающие отношение конвеpтиpуемости.
B2--2. Напомним комбинаторную характеристику используемого объекта:(B) Bxyz = x(yz).
B2--3. Применяя эту схему к a(bcd), получим:
a(bcd) = Ba(bc)d ( по схеме (B))
= B(Ba)bcd ( по схеме (B))
= BBBabcd. ( по схеме (B))
Учитывая постулаты, имеем: BBBabcd = a(bcd), т.е. B2 = BBB.
Ответ. Объект B2 с комбинаторной характеристикой
B2abcd = a(bcd)
имеет вид B2 = BBB.
Задача 2.6 Вывод выражения для комбинатора B3.
Формулировка задачи. Выpазить чеpезK иS и другие предваритель-
но определенные объекты объект с комбинатоpной хаpактеpистикой:
B3abcde = a(bcde), (B3)
Решение.
B3--1. Сфоpмулиpуем постулаты, задающие отношение конвеpтиpуемости.
B3--2. Напомним комбинаторные характеристики используемых объектов:(B) Bxyz = x(yz), (B2) B2xyzw = x(yzw).
B3--3. Применяя эти схемы к a(bcde), получим:
a(bcde) = B2a(bc)de ( по схеме (B2))
= B(B2a)bcde ( по схеме (B))
= BBB2abcde. ( по схеме (B))
Учитывая постулаты, имеем: BBB2abcde = a(bcde)
, т.е.
B3 = BBB2.
Ответ. ОбъектB3 с комбинаторной характеристикойB3abcde = a(bcde)
имеет вид B3 = BBB2.
Задача 2.7 Вывод выражения для комбинатора C[2].
Формулировка задачи. Выpазить чеpезK иS и другие предваритель-
но определенные объекты объект с комбинатоpной хаpактеpистикой:
C[2]abcd = acdb, (C[2])
Решение.
C[2]--1. Сфоpмулиpуем постулаты, задающие отношение конвеpтиpу-
емости.
C[2]--2. Напомним комбинаторные характеристики, возможно, ис-
пользуемых объектов: (B) Bxyz = x(yz), (C) Cxyz = xzy.
C[2]--3. Применяя эти схемы к acdb, получим:
acdb = C(ac)bd ( по схеме (C))
= BCacbd ( по схеме (B))
= C(BCa)bcd ( по схеме (C))
= BC(BC)acbd. ( по схеме (B))
Учитывая постулаты, имеем: BC(BC)acbd = acbd, то есть C[2] =
BC(BC).
Ответ. Объект C[2] с комбинаторной характеристикой C[2]abcd =
acbd
имеет вид C[2] = BC(BC).
Задача 2.8 Вывод выражения для комбинатора C[2].
Формулировка задачи. Выpазить чеpезK иS и другие предваритель-
но определенные объекты объект с комбинатоpной хаpактеpистикой:
C[2]abcd = adbc, (C[2])
Решение.
C[2]--1. Сфоpмулиpуем необходимые постулаты.
C[2]--2. Запишем комбинаторные характеристики, возможно, ис-
пользуемых объектов: (B2) B2xyzw = x(yzw), (C) Cxyz =
xzy.
C[2]--3. Применяя эти схемы к adbc, получим:
adbc = Cabdc ( по схеме (C))
= C(Cab)cd ( по схеме (C))
= B2CCabcd. ( по схеме (B2))
Учитывая постулаты, имеем: B2CCabcd = adbc
, т.е. C[2] = B2CC.
Ответ. Объект C[2] с комбинаторной характеристикой C[2]abcd =
adbc имеет вид C[2] = B2CC.
Задача 2.9 Вывод выражения для комбинатора C[3].
Формулировка задачи. Выpазить чеpезK иS и другие предваритель-
но определенные объекты объект с комбинатоpной хаpактеpистикой:
C[3]abcde = acdeb, (C[3])
Решение.
C[3]--1. Сфоpмулиpуем необходимые постулаты.
C[3]--2. Запишем комбинаторные характеристики, возможно, ис-
пользуемых объектов: (B) Bxyz = x(yz), (C) Cxyz =
xzy, (C[2]) Cxyzw = xzwy.
C[3]--3. Применяя эти схемы к acdeb, получим:
acdeb = C[2](ac)bde ( по схеме (C[2]))
= BC[2]acbde ( по схеме (B))
= C(BC[2]a)bcde ( по схеме (C))
= BC(BC[2])abcde. ( по схеме (B))
Учитывая постулаты, имеем:BC(BC[2])abcde = acdeb, то есть C[3] =
BC(BC[2]).
Ответ. Объект C[3] с комбинаторной характеристикой C[3]abcde =
acdeb имеет вид C[3] = BC(BC[2]).
Задача 2.10 Вывод выражения для комбинатора C[3].
Формулировка задачи. Выpазить чеpезK иS и другие предваритель-
но определенные объекты объект с комбинатоpной хаpактеpистикой:
C[3]abcde = aebcd, (C[3])
Решение.
C[3]--1. Сфоpмулиpуем постулаты.
C[3]--2. Запишем комбинаторные характеристики, возможно, ис-
пользуемых объектов:(B2) B2xyzw = x(yzw), (C) Cxyz =
xzy, (C[2]) C[2]xyzw = xwyz.
Применяя эти схемы к aebcd, получим:
aebcd = Cabecd ( по схеме (C))
= C[2](Cab)cde ( по схеме (C[2]))
= B2C[2]Cabcde. ( по схеме (B2))
Учитывая постулаты, имеем: B2C[2]Cabcde = aebcd
, то есть C[3] =
B2C[2]C
.
Ответ. Объект C[3] с комбинаторной характеристикой C[3]abcde =
aebcd
имеет вид C[3] = B2C[2]C.
Задача 2.11 Вывод выражения для комбинатора Φ.
Формулировка задачи. Выpазить чеpезK иS и другие предваритель-
но определенные объекты объект с комбинатоpной хаpактеpистикой:
Φabcd = a(bd)(cd), (Φ)
Решение.
Φ--1. Сфоpмулиpуем необходимые постулаты, задающие отноше-
ние конвеpтиpуемости.
Φ--2. Запишем комбинаторные характеристики, возможно, используе-
мых объектов: (B2) B2xyzw = x(yzw), (B) Bxyz =
x(yz), (S) Sxyz = xz(yz).
Φ--3. Применяя эти схемы к a(bd)(cd), получим:
a(bd)(cd) = Babd(cd) ( по схеме (B))
= S(Bab)cd ( по схеме (S))
= B2SBabcd. ( по схеме (B2))
Учитывая постулаты, имеем: B2SBabcd = a(bd)(cd)
, то есть Φ =
B2SB
.
Ответ. ОбъектΦс комбинаторной характеристикойΦabcd = a(bd)(cd)
имеет вид Φ = B2SB.
Задача 2.12 Вывод выражения для комбинатора Y .
Формулировка задачи. Выpазить чеpезK иS и другие предваритель-
но определенные объекты объект с комбинатоpной хаpактеpистикой:
Y a = a(Y a), (Y )
Решение.
Y --1. Сфоpмулиpуем необходимые постулаты, задающие отноше-
ние конвеpтиpуемости.
Y --2. Запишем комбинаторные характеристики, возможно, исполь-
зуемых объектов:(S) Sxyz = xz(yz), (W) W xy = xyy, (B) Bxyz =
x(yz).
Y --3. Докажем, что Y = W S(BW B).
Y a = W S(BW B)a ( по предположению)
= S(BW B)(BW B)a ( по схеме (W))
= BW Ba(BW Ba) ( по схеме (S))
= W(Ba)(BW Ba) ( по схеме (B))
= Ba(BW Ba)(BW Ba) ( по схеме (W))
= a(BW Ba(BW Ba)) ( по схеме (B))
= a(S(BW B)(BW B)a) ( по схеме (S))
= a(W S(BW B)a) ( по схеме (W))
= a(Y a). ( по предположению)
Следовательно, одно из представлений объектаY таково: Y = W S(BW B).
Ответ. Объект Y с комбинаторной характеристикой Y a = a(Y a)
имеет вид Y = W S(BW B).
|