Для достижения полной ленивости нет необходимости производить
вычисления тех выражений, которые не содержат (свободных) вхо-
ждений формального параметра.
Определение 16.2 Выражение E называется собственным подвы-
ражением F, если и только если E является подвыражением F и E
не совпадает с F.
Определение 16.3 Подвыражение E из абстракции считается сво-
бодным вL, если все переменные E свободны вL.
Определение 16.4 . Максимально свободное выражение (МСВ) вL-
это такое свободное выражение, которое не является собственным
подвыражением другого свободного выражения в L.
Пример 16.12 В приводимых ниже абстракциях подчеркнуты МСВ:
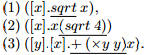
Для обеспечения полной ленивости при выполнении β-редукции не
следует означивать максимально свободные абстракции.
Пример 16.13 Вернемся к функции из примера 16.11:
letrec f = g 4
g = [x].[y].+ y (sqrt x)
in + (f 1)(f 2)
Последовательность редукций начинается, как в этом примере:
+ (f 1)(f 2) → + (. 1)(. 2)
−→ (([x].[y].+ y(sqrt x))4)
→ + (. 1)(. 2)
−→ ([y].+ y (sqrt 4))
(здесь: выражение (sqrt 4) является МСВ в [y].-абстракции, поэто-
му при приложении [y]. к аргументу (sqrt 4) не следует вычислять
→ + (. 1)(+ 2 .)
−→ ([y].+ y (sqrt 4)) )
Означивание имеет указатель на (sqrt 4) в теле абстракции:
→ + (. 1)(+ 2 .)
−→ ([y].+ y 2)
→ + (. 1)4
−→ ([y].+ y 2)
→ + (+ 1 2)4
→ + 3 4
→ 7
В этом случае (sqrt 4) вычисляется только один раз.
Упражнение 16.10 Вычислить выражение из упражнения 16.9, вос-
пользовавшись МСВ. |